Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
Ćwiczenie 2
Ćwiczenie 3
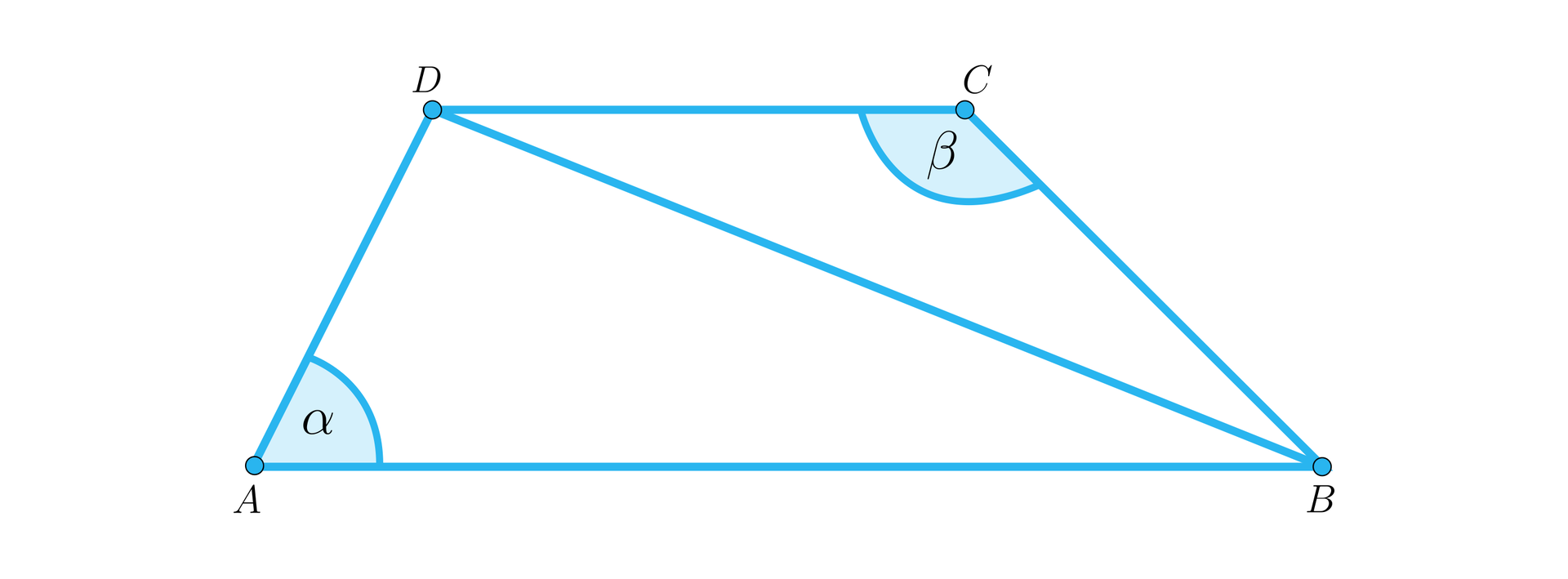
Dany jest trapez , w którym . Jego przekątna ma długość dwa razy krótszą niż każdy z promieni okręgów opisanych na trójkątach i . Wyznacz miary kątów trapezu.
Ćwiczenie 4
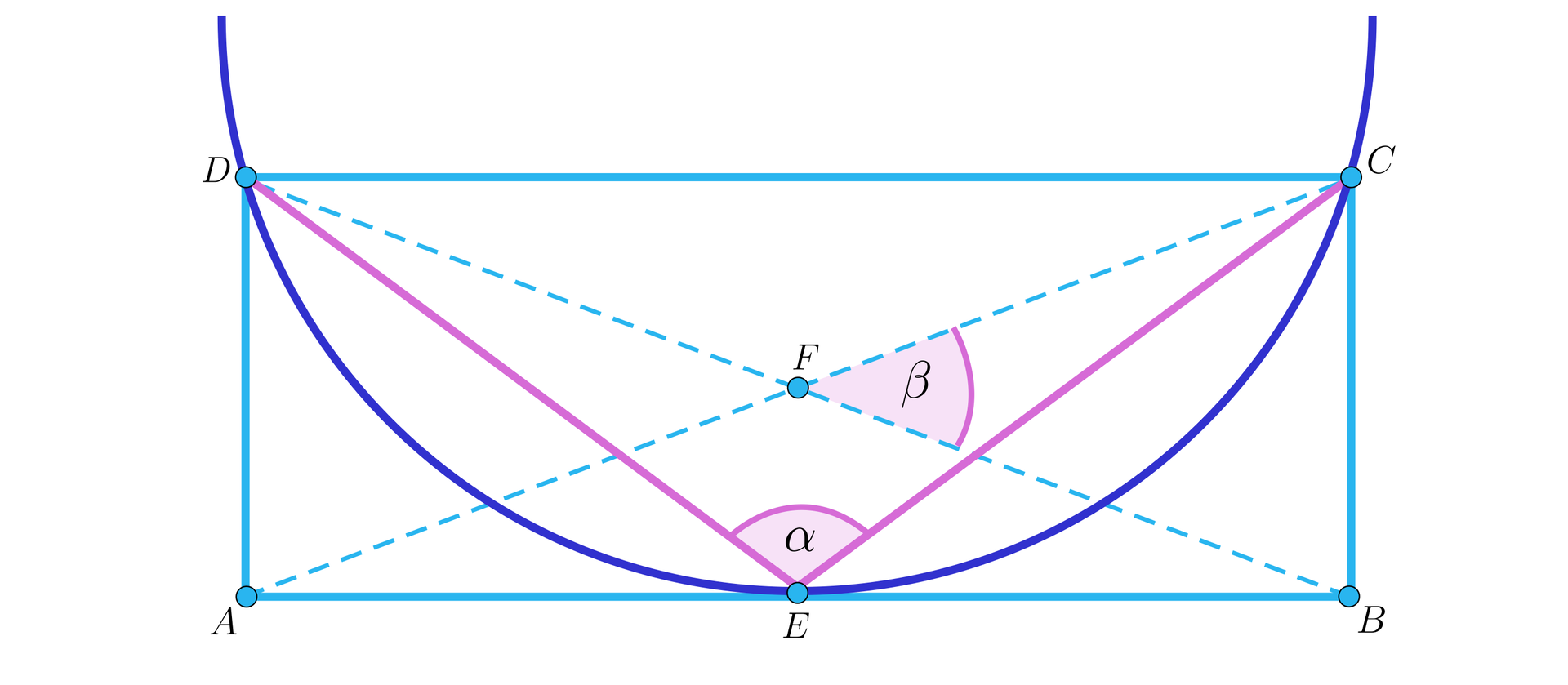
Punkt jest środkiem boku prostokąta . Bok ma długość . Promień okręgu opisanego na trójkącie jest równy , a środek tego okręgu leży na zewnątrz tego prostokąta. Wyznacz przybliżoną miarę kąta, pod jakim przecinają się przekątne prostokąta.
Ćwiczenie 5
Ćwiczenie 6
Ćwiczenie 7
Ćwiczenie 8
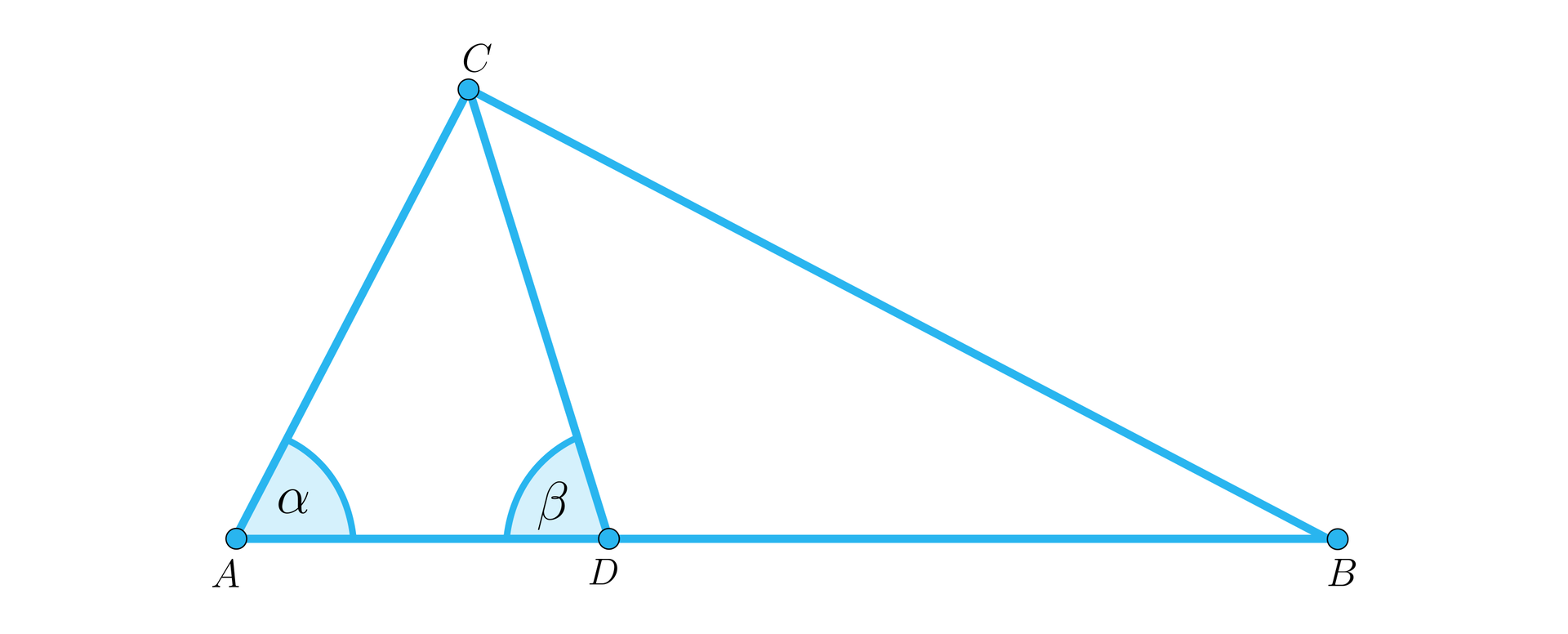
Dwusieczna kąta prostego w trójkącie prostokątnym podzieliła jego przeciwprostokątną na odcinki o długości i . Oblicz, z dokładnością do , miary kątów ostrych tego trójkąta.