Sprawdź się
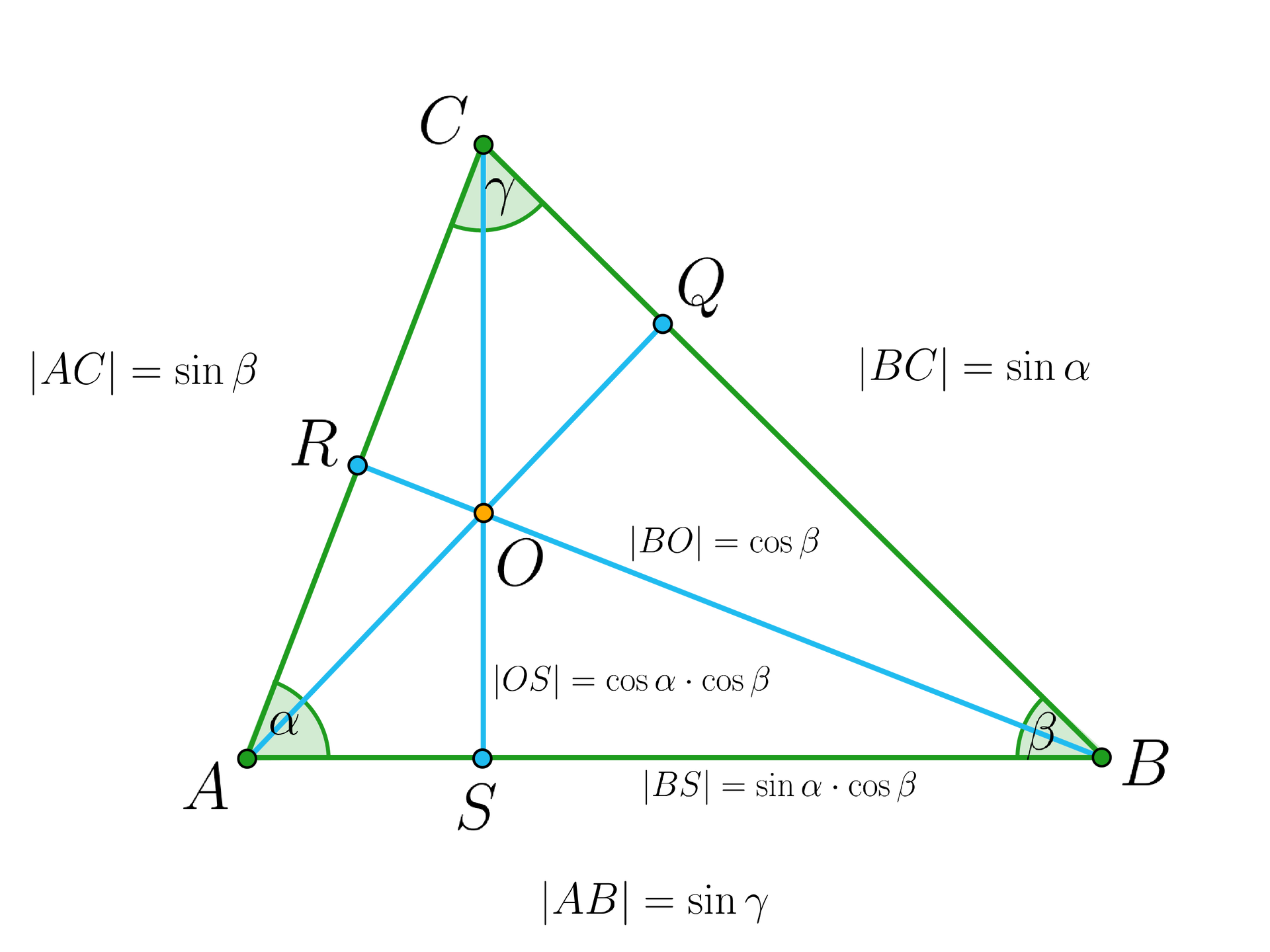
Korzystając z modelu opisanego na powyższym rysunku i oznaczeń tam przyjętych, wyznacz długość odcinka , a następnie wykaż, że w dowolnym trójkącie o kątach , , zachodzi nierówność .
Uzupełnij puste pola, dobierając odpowiedni tekst (oznaczenia) spośród podanych niżej.
Stąd .
Ale z nierówności trójkąta (dla trójkąta ) mamy w szczególności,
że 1. , 2. , 3. , 4. , 5. , 6. 1. , 2. , 3. , 4. , 5. , 6. , a stąd wynika teza.
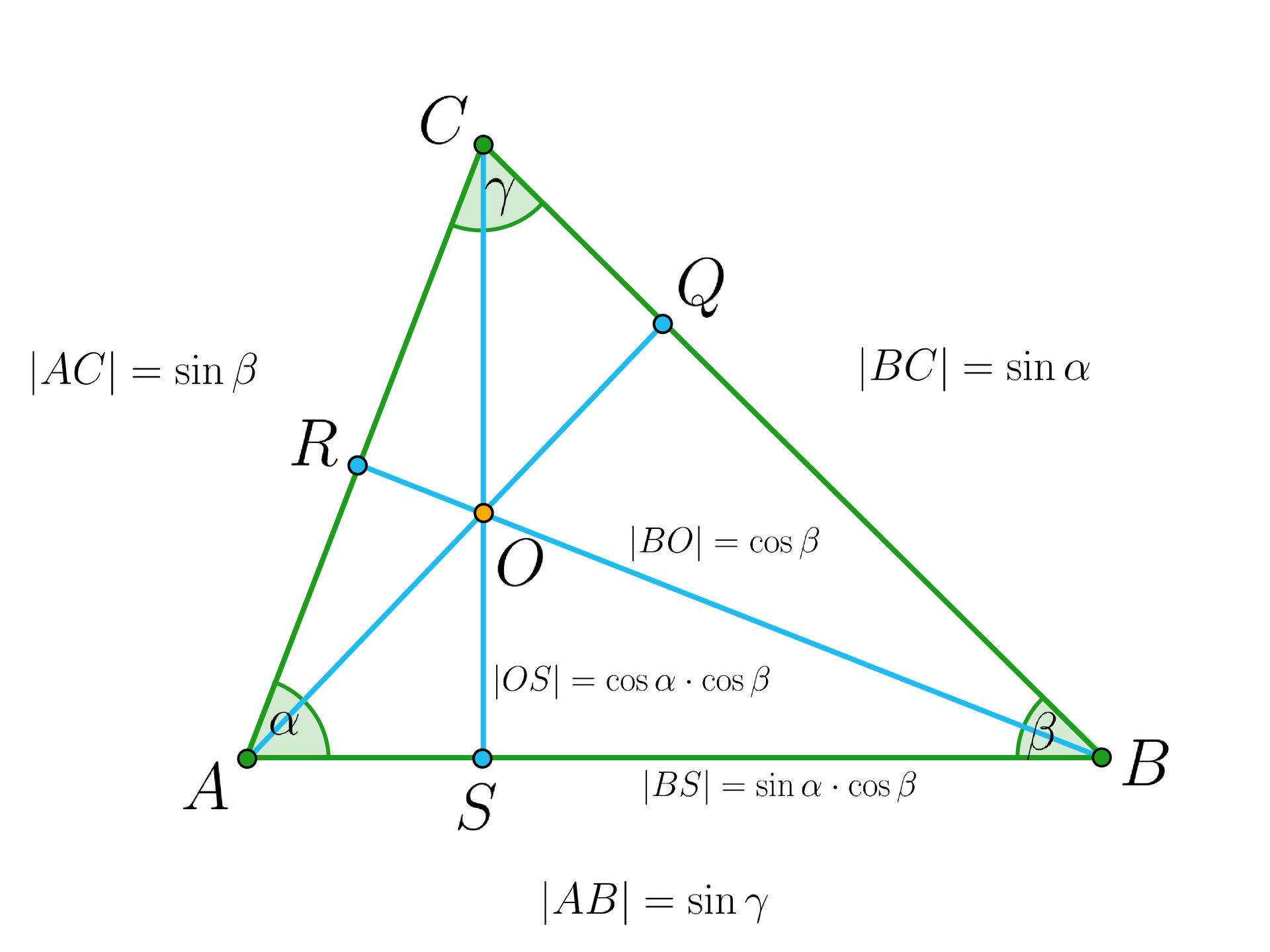
Wiedząc, że dla dowolnego kąta prawdziwy jest wzór oraz korzystając z modelu opisanego na rysunku i oznaczeń tam przyjętych, wyznacz długość odcinków oraz , a następnie wykaż, że w dowolnym trójkącie o kątach , , zachodzi równość .
Zapisz dowód modyfikując kolejność poniższych sformułowań.
Udowodnij, że jeśli w trójkącie rozwartokątnym kąty mają miary , , i jest kątem o największej mierze, to . Wskazówka: zauważ, że boki dowolnego trójkąta wpisanego w okrąg o średnicy 1 mają długości równe sinusom kątów leżących naprzeciwko tych boków.
Udowodnij, że w trójkącie ostrokątnym, w którym kąty mają miary , , , prawdziwa jest nierówność .
Punkt jest ortocentrum trójkąta ostrokątnego . Udowodnij, że promień okręgu opisanego na trójkącie jest równy promieniowi okręgu opisanego na trójkącie .
W danym trójkącie, dwusieczna jednego z jego kątów podzieliła bok przeciwległy na odcinki o długościach i . Uzasadnij, ze żaden z boków tego trójkąta nie może mieć długości .