Zapisywanie treści prostych zadań za pomocą równań
Co to jest równanie?
Z równaniami spotykaliście się już w młodszych klasach. Z pewnością często znajdowaliście liczbę ukrytą pod znakiem zapytania, chmurką czy w okienku, na przykład:
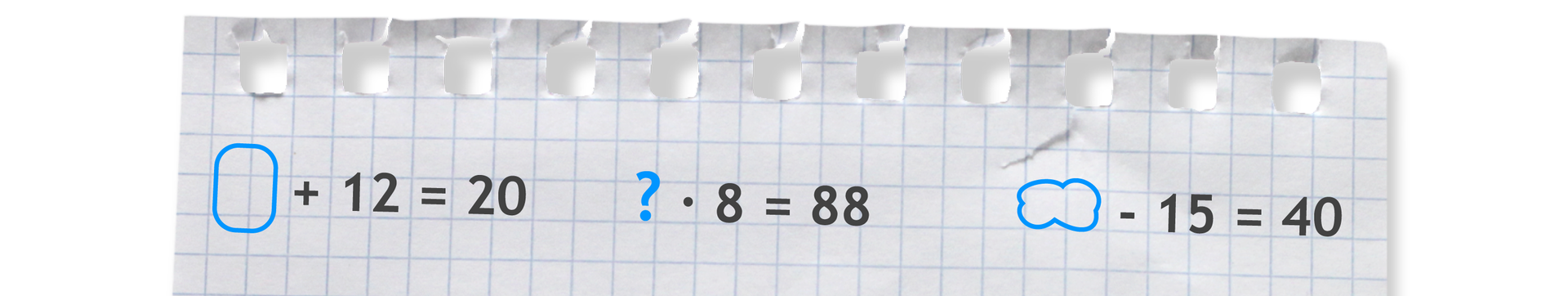
Jeżeli w tych równościach zastąpimy okienko, chmurkę czy znak zapytania dowolną literą, to otrzymamy równania.
W równaniach litera oznacza szukaną liczbę. Nazywamy ją niewiadomą.
Układanie prostych równań
Agatka ma o kredek więcej od Jacka. Razem mają kredki. Ile kredek ma Jacek?
Ułóżmy równanie odpowiadające treści tego zadania i znajdźmy odpowiedź na pytanie.
sposób
Oznaczmy liczbę kredek Jacka przez .
Wówczas liczba kredek Agatki to .
Łączna liczba kredek obojga dzieci to .
Z treści zadania wiemy także, że razem mają oni kredki.
Możemy więc zapisać równanie:
Jest to proste równanie, więc łatwo możemy odgadnąć, że pod literą ukryta jest liczba .
Odp.: Jacek ma kredek.
sposób
Treść tego zadania mogliśmy zapisać także nieco inaczej, oznaczając jako liczbę kredek Agatki.
- liczba kredek Agatki
- liczba kredek Jacka
- łączna liczba kredek
Teraz równanie ma postać:
Pod literą ukryta jest liczba , czyli liczba kredek Agatki.
Liczba kredek Jacka to , czyli .
Układając równanie nie wpisujemy jednostek, ale występujące w nim liczby powinny być wyrażone w tych samych jednostkach.
Mamy zadanie:
Ania kupiła jeden jogurt i bułek po . Razem zapłaciła . Ile kosztował jogurt?
Do zadania możemy ułożyć równanie:

Oczywiście oznacza cenę jogurtu. Czy wiesz, ile kosztuje jogurt?
Film dostępny pod adresem https://zpe.gov.pl/a/D2fs2mq4m
Animacja
Film dostępny pod adresem https://zpe.gov.pl/a/D2fs2mq4m
Animacja
Przeciągnij i upuść odpowiednie liczby lub symbole działań.
, , , , , , , , , , ,
a) Jeśli liczbę powiększymy o , to otrzymamy . Jaką liczbą jest ?
............ ............
............
b) Jeśli liczbę pomiejszymy o , to otrzymamy . Jaką liczbą jest ?
............ ............
............
c) Jeśli liczbę powiększymy dwukrotnie, to otrzymamy . Jaką liczbą jest ?
............ ............
............
d) Jeśli liczbę zmniejszymy razy, to otrzymamy . Jaką liczbą jest ?
............ ............
............
Dobieranie równań do treści zadania
Przeciągnij i upuść równanie do zadania, które ono opisuje.
, , , , ,
a) Za ołówki, każdy po groszy oraz zeszyty po złotych za sztukę, zapłacono 13 złotych.
..........................
b) Samochodzik jest o złote tańszy od piłki, która kosztuje złotych. Za samochodziki i piłki zapłacono złotych.
..........................
c) Ewa jest o lat starsza od Kasi, która ma lat. Razem mają lat.
..........................
Co w równaniu oznacza niewiadoma?
Wskaż prawidłową odpowiedź.
Kamil ma razy więcej płyt niż Bartek, który ma o płyt więcej niż Dawid. Razem mają płyty.
. Możliwe odpowiedzi: 1. liczba płyt Kamila, 2. liczba płyt Bartka, 3. liczba płyt Dawida
Do treści zadania ułożono równanie. Co oznacza niewiadoma w danym równaniu?
Wskaż prawidłową odpowiedź.
Kamil ma razy więcej płyt niż Bartek, który ma o płyt więcej niż Dawid. Razem mają płyty.
.
- liczba płyt Kamila
- liczba płyt Bartka
- liczba płyt Dawida
Wskaż prawidłową odpowiedź.
Szkolna drużyna piłki nożnej zdobyła w rozgrywkach goli. Wszystkie bramki strzelili trzej zawodnicy. Najlepszym strzelcem okazał się Marek, który zdobył o gole więcej od Andrzeja, a Piotr zdobył bramki. Możliwe odpowiedzi: 1. liczba goli Marka, 2. liczba goli Andrzeja, 3. liczba goli Piotra
Do treści zadania ułożono równanie. Co oznacza niewiadoma w danym równaniu?
Wskaż prawidłową odpowiedź.
Szkolna drużyna piłki nożnej zdobyła w rozgrywkach goli. Wszystkie bramki strzelili trzej zawodnicy. Najlepszym strzelcem okazał się Marek, który zdobył o gole więcej od Andrzeja, a Piotr zdobył bramki.
- liczba goli Marka
- liczba goli Andrzeja
- liczba goli Piotra
Wskaż prawidłową odpowiedź.
Za 5 kg truskawek po za kilogram Ania zapłaciła o więcej niż za malin.
. Możliwe odpowiedzi: 1. cena truskawek, 2. wartość całych zakupów, 3. cena malin
Do treści zadania ułożono równanie. Co oznacza niewiadoma w danym równaniu?
Wskaż prawidłową odpowiedź.
Za 5 kg truskawek po za kilogram Ania zapłaciła o więcej niż za malin.
.
- cena truskawek
- wartość całych zakupów
- cena malin
Jurek ma o książek więcej niż Agata i razy więcej niż Iza. Jurek, Agata i Iza maja łącznie tyle książek ile Gosia i Ania razem. Gosia ma książek, a Ania tyle co Agata.
Wybierz, co oznacza niewiadoma w poszczególnych równaniach.
liczba książek Agaty, liczba wszystkich książek, liczba książek Izy, liczba książek Gosi, liczba wszystkich książek, liczba książek Gosi, liczba książek Agaty, liczba książek Agaty, liczba książek Izy, liczba książek Jurka, liczba wszystkich książek, liczba książek Jurka, liczba książek Gosi, liczba książek Jurka, liczba książek Izy
a) ......................................................
b) ......................................................
c) ......................................................