Liczby wymierne. Wartość bezwzględna
Zimą możemy zaobserwować, że temperatura powietrza spada poniżej . Mówimy wówczas, że jest równa, na przykład , , . Liczby, za pomocą których zapisana jest ta temperatura, nazywamy ujemnymi.

Film dostępny na portalu epodreczniki.pl
Animacja
Wysokość bezwzględna to pionowa odległość (wysokość) danego punktu względem przyjętego punktu odniesienia, którym jest średni poziom morza. Wysokość bezwzględna oznaczana jest skrótem n.m.p., czyli nad poziomem morza (Wikipedia).
Wysokość bezwzględną punktów leżących powyżej poziomu morza oznaczamy liczbami dodatnimi, a punktów leżących poniżej poziomu morza, tzw. depresji, liczbami ujemnymi.
Najniższy obszar na lądzie na kuli ziemskiej stanowi depresja Morza Martwego (dom p.p.m, czyli do – m n.p.m)
Dotychczas poznaliśmy:
liczby naturalne : , …
liczby całkowite: …, , …

Film dostępny na portalu epodreczniki.pl
Animacja
Liczba wymierna to liczba, którą można przedstawić w postaci ułamka gdzie i są liczbami całkowitymi i .
Liczbami wymiernymi są liczby naturalne, całkowite i ułamki.

Odwrotnością liczby jest liczba , ponieważ zamieniając liczbę na ułamek niewłaściwy, otrzymamy ułamek . Analogicznie parami liczb wzajemnie odwrotnych są
i
i
i
Liczba odwrotna do danej liczby , to taka liczba , że
Odwrotnością liczby , gdzie jest liczba .
Iloczyn liczb wzajemnie odwrotnych jest równy .
Przykład
Liczba odwrotna do liczby to bo .
Zaznaczmy na osi liczbowej pary liczb.
i
i
i
RhtAFz3tNaYjb1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Co możemy powiedzieć o odległościach liczb i od zera? Zauważmy, że te odległości są równe . Podobnie odległość każdej z liczb i od zera wynosi a liczb i wynosi . Liczby i , i oraz i to pary liczb przeciwnych.
Liczba przeciwna do danej liczby to taka liczba , że zachodzi równość
Liczby przeciwne to takie liczby, które znajdują się po przeciwnych stronach na osi liczbowej i których odległość od jest taka sama.
Wartość bezwzględna liczby jest to odległość liczby od zera na osi liczbowej.

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia dwie osie liczbowe z zaznaczonymi punktami od -6 do 6. Na pierwszej osi zaznaczona odległość liczby 5 od liczby 0, równa 5. Zapis: wartość bezwzględna z liczby 5 =5. Na drugiej osi zaznaczona odległość liczby -4 od liczby 0, równa 4. Zapis: wartość bezwzględna z liczby -4 =4.
Własności wartości bezwzględnej
Jeżeli liczba jest nieujemna, to jej wartością bezwzględną jest ta sama liczba .
Jeżeli jest ujemna , to jej wartością bezwzględną jest liczba przeciwna do , czyli .
Wartość bezwzględną liczby oznaczamy .
Liczby przeciwne mają taką samą wartość bezwzględną.
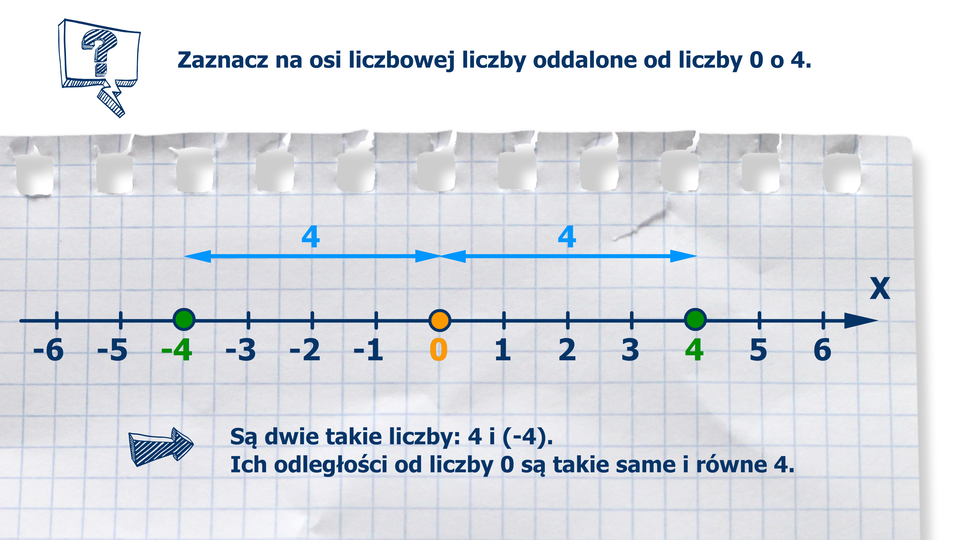
Film dostępny na portalu epodreczniki.pl
Animacja przedstawia oś liczbową z zaznaczonymi punktami od -6 do 6. Należy zaznaczyć liczby oddalone od liczby 0 o 4. Są dwie takie liczby: 4 i -4. Ich odległości od liczby 0 są takie same i wynoszą 4.
Rozwiążemy równanie , gdzie

Film dostępny na portalu epodreczniki.pl
Animacja pokazuje rozwiązanie równania: wartość bezwzględna z liczby x =a, gdzie a większe lub równe 0. Szukamy takich liczb, których odległość od liczby 0 jest równa a. Na osi zaznaczona odległość liczby a od liczby 0, równa a oraz odległość liczby –a od liczby 0, równa a. Zapis: Niech a większe lub równe 0. Rozwiązaniem równania wartość bezwzględna z liczby x =a jest x =a lub x =-a.
Uzasadnij, że podana liczba jest wymierna.
Rozstrzygnij, które zdanie jest prawdziwe, a które fałszywe.
| Prawda | Fałsz | |
| Liczbą odwrotną do jest liczba | □ | □ |
| Odwrotność liczby naturalnej nie jest liczbą wymierną. | □ | □ |
| Iloczyn liczby i liczby do niej przeciwnej wynosi. | □ | □ |
| Suma liczby i liczby do niej przeciwnej wynosi. | □ | □ |
Zaznacz daną liczbę na osi liczbowej. Pamiętaj o odpowiednim doborze jednostki.
Odczytaj liczby, które odpowiadają punktom na osi liczbowej.

Przeciągnij liczby z dolnej sekcji do górnej.
<span aria-label=" minus, dziesięć" role="math"><math><mo>-</mo><mn>10</mn></math></span>, <span aria-label=" minus, zero przecinek zero dwa zero" role="math"><math><mo>-</mo><mn>0,(2)</mn></math></span>, <span aria-label="początek ułamka, dwadzieścia jeden, mianownik, siedem, koniec ułamka" role="math"><math><mfrac><mrow><mn>21</mn></mrow><mrow><mn>7</mn></mrow></mfrac></math></span>, <span aria-label=" minus, początek ułamka, dwanaście, mianownik, trzy, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>12</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label=" minus, początek ułamka, pięć, mianownik, dwa, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>5</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label="dwanaście" role="math"><math><mn>12</mn></math></span>, <span aria-label=" minus, początek ułamka, dwanaście, mianownik, trzy, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>12</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label="początek ułamka, dwadzieścia jeden, mianownik, siedem, koniec ułamka" role="math"><math><mfrac><mrow><mn>21</mn></mrow><mrow><mn>7</mn></mrow></mfrac></math></span>, <span aria-label="jeden przecinek jeden" role="math"><math><mn>1,1</mn></math></span>, <span aria-label="pięć" role="math"><math><mn>5</mn></math></span>, <span aria-label="jeden" role="math"><math><mn>1</mn></math></span>, <span aria-label=" minus, pięć" role="math"><math><mo>-</mo><mn>5</mn></math></span>, <span aria-label=" minus, dziesięć" role="math"><math><mo>-</mo><mn>10</mn></math></span>, <span aria-label=" minus, pięć" role="math"><math><mo>-</mo><mn>5</mn></math></span>, <span aria-label="początek ułamka, osiem, mianownik, dwa, koniec ułamka" role="math"><math><mfrac><mrow><mn>8</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label="początek ułamka, zero, mianownik, trzy, koniec ułamka" role="math"><math><mfrac><mrow><mn>0</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label="jeden" role="math"><math><mn>1</mn></math></span>, <span aria-label=" minus, dziesięć" role="math"><math><mo>-</mo><mn>10</mn></math></span>, <span aria-label=" minus, początek ułamka, dwanaście, mianownik, trzy, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>12</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label="dwanaście" role="math"><math><mn>12</mn></math></span>, <span aria-label="dwanaście" role="math"><math><mn>12</mn></math></span>, <span aria-label=" minus, dziesięć" role="math"><math><mo>-</mo><mn>10</mn></math></span>, <span aria-label=" minus, początek ułamka, sześć, mianownik, dwa, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>6</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label="pięć" role="math"><math><mn>5</mn></math></span>, <span aria-label=" minus, początek ułamka, pięć, mianownik, dwa, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>5</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label="początek ułamka, osiem, mianownik, dwa, koniec ułamka" role="math"><math><mfrac><mrow><mn>8</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label=" minus, pięć" role="math"><math><mo>-</mo><mn>5</mn></math></span>, <span aria-label="początek ułamka, zero, mianownik, trzy, koniec ułamka" role="math"><math><mfrac><mrow><mn>0</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label=" minus, pięć" role="math"><math><mo>-</mo><mn>5</mn></math></span>, <span aria-label=" minus, początek ułamka, sześć, mianownik, dwa, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>6</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label=" minus, początek ułamka, sześć, mianownik, dwa, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>6</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label="pięć" role="math"><math><mn>5</mn></math></span>, <span aria-label="jeden" role="math"><math><mn>1</mn></math></span>, <span aria-label="początek ułamka, dwadzieścia jeden, mianownik, siedem, koniec ułamka" role="math"><math><mfrac><mrow><mn>21</mn></mrow><mrow><mn>7</mn></mrow></mfrac></math></span>, <span aria-label="początek ułamka, zero, mianownik, trzy, koniec ułamka" role="math"><math><mfrac><mrow><mn>0</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label="początek ułamka, osiem, mianownik, dwa, koniec ułamka" role="math"><math><mfrac><mrow><mn>8</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label=" minus, początek ułamka, dwanaście, mianownik, trzy, koniec ułamka" role="math"><math><mo>-</mo><mfrac><mrow><mn>12</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label=" minus, zero przecinek zero dwa zero" role="math"><math><mo>-</mo><mn>0,(2)</mn></math></span>
| Naturalne | |
|---|---|
| Całkowite | |
| Wymierne | |
| Ujemne | |
| Mniejsze od |
Wszystkie liczby całkowite wybrane ze zbioru liczb, , , , , , , , to
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Każda liczba naturalna jest liczbą wymierną.
- Każda liczba wymierna jest liczbą całkowitą.
- W zbiorze liczb całkowitych nie ma najmniejszej liczby.
- nie jest liczbą wymierną.
Oblicz.
Przeciągnij pasujące elementy z sekcji dolnej do górnej.
<span aria-label=" minus, trzy kropka pięć" role="math"><math><mo>-</mo><mn>3</mn><mo>,</mo><mn>5</mn></math></span> i <span aria-label="początek ułamka, siedem, mianownik, dwa, koniec ułamka" role="math"><math><mfrac><mrow><mn>7</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math></span>, <span aria-label="początek ułamka, jeden, mianownik, cztery, koniec ułamka" role="math"><math><mfrac><mrow><mn>1</mn></mrow><mrow><mn>4</mn></mrow></mfrac></math></span> i <span aria-label="cztery" role="math"><math><mn>4</mn></math></span>, <span aria-label="dwa kropka dwa" role="math"><math><mn>2</mn><mo>,</mo><mn>2</mn></math></span> i <span aria-label="początek ułamka, pięć, mianownik, jedenaście, koniec ułamka" role="math"><math><mfrac><mrow><mn>5</mn></mrow><mrow><mn>11</mn></mrow></mfrac></math></span>, <span aria-label=" minus, dwa kropka cztery" role="math"><math><mo>-</mo><mn>2</mn><mo>,</mo><mn>4</mn></math></span> i <span aria-label="początek ułamka, dwanaście, mianownik, pięć, koniec ułamka" role="math"><math><mfrac><mrow><mn>12</mn></mrow><mrow><mn>5</mn></mrow></mfrac></math></span>, <span aria-label="zero kropka trzy siedem pięć" role="math"><math><mn>0</mn><mo>,</mo><mn>375</mn></math></span> i <span aria-label="początek ułamka, osiem, mianownik, trzy, koniec ułamka" role="math"><math><mfrac><mrow><mn>8</mn></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>
| Liczby przeciwne | |
|---|---|
| Liczby odwrotne |
Odwrotnością liczby jest liczba
Liczbą przeciwną do jest
Oblicz wartość wyrażenia . Liczba odwrotna do otrzymanej liczby, to
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Suma liczby i liczby do niej przeciwnej wynosi .
- Iloczyn liczby i liczby do niej przeciwnej wynosi .
- Odwrotność liczby naturalnej różnej od zera nie jest liczbą wymierną.
- Liczbą przeciwną do odwrotności liczby jest liczba .
Wybierz.
naturalną, nieskończone nieokresowe, dodatnią, wymierna, dodatniej, ujemnej, naturalna, skończone
Każda liczba .................................................. jest liczbą całkowitą. Liczba przeciwna do liczby całkowitej .................................................. jest liczbą naturalną. Odwrotność liczby naturalnej różnej od zera jest liczbą ................................................... Liczba, która ma rozwinięcie dziesiętne .................................................. nie jest liczbą wymierną.
