Przeczytaj

Miejsce geometryczne punktów, z których dany odcinek widać pod stałym kątem

Pojęcie „miejsca geometrycznego” oznacza zbiór wszystkich punktów płaszczyzny lub przestrzeni, które spełniają z góry zadany warunek.

Kątem, pod którym dany odcinek $A B$ widać z określonego punktu $C$ nazywamy kąt wypukły, którego ramiona zawierają odcinki $C A$ i $C B$ . Jego miara wyznacza tzw. rozmiar kątowyrozmiar kątowyrozmiar kątowy danego obiektu.

R1eXBlv5ZuIcj

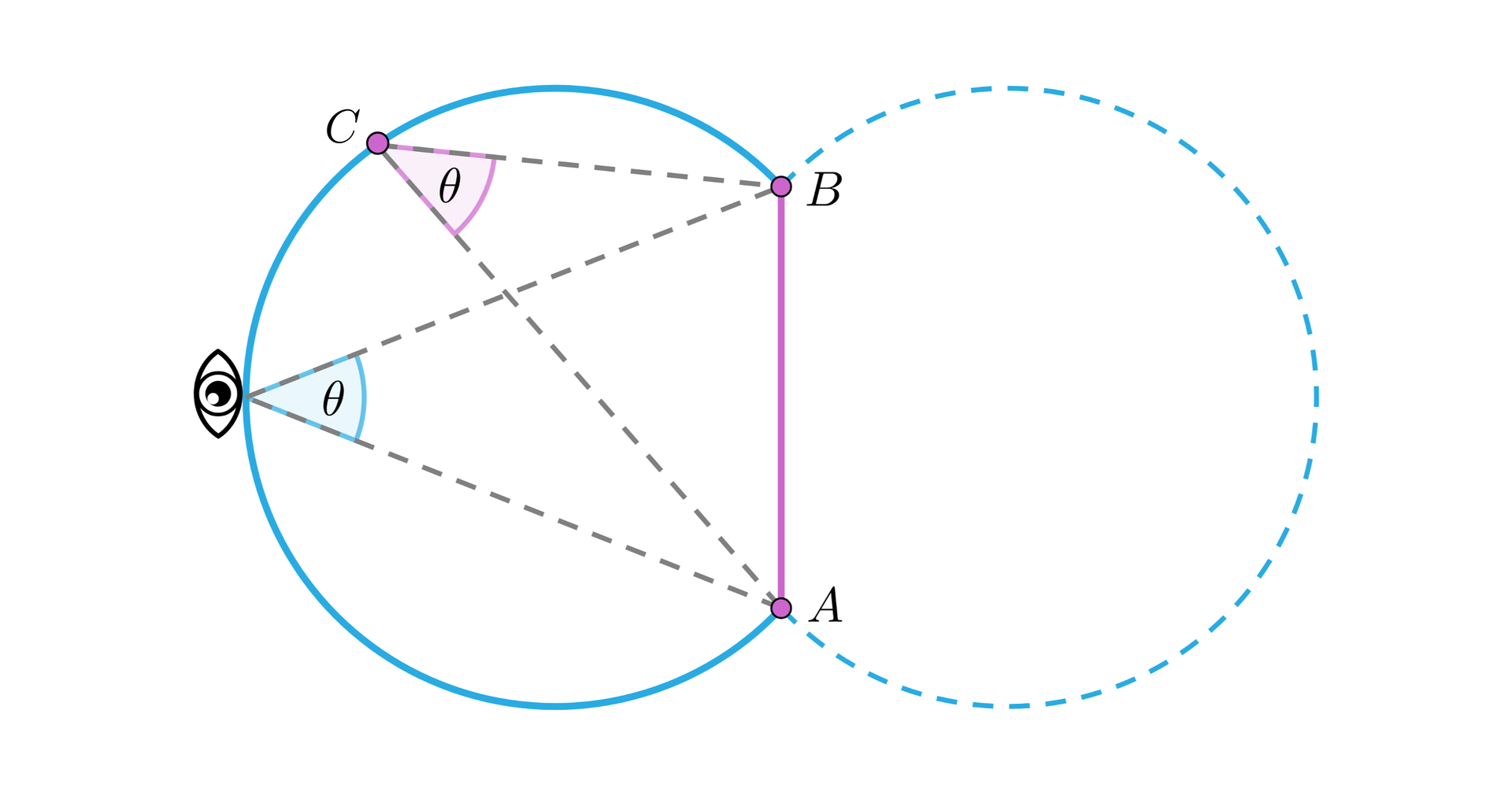
Grafika przedstawia dwa okręgi, które nachodzą na siebie. Jeden z nich jest narysowany linią ciągłą, a drugi przerywaną. Punkty w których stykają się okręgi są oznaczone literami: A oraz B. Odcinek AB ma kolor różowy. Na okręgu narysowanym linią ciągłą zaznaczone są dwa punkty. Jeden podpisany jest literą C, natomiast koło drugiego narysowane jest oko. Punkt C, razem z punktami A oraz B tworzy trójkąt. Przy czym kąt między bokami AC i BC jest podpisany literą θ. Punkt zaznaczony rysunkiem oka z punktami A i B również tworzy trójkąt. Kąt między ramionami, których jednym z wierzchołków jest oko, jest podpisany literą θ. — Rozmiar kątowy

Okazuje się, że miejscem geometrycznym punktów, z których dany odcinek widać pod stałym kątem jest łuk okręgu, którego końcami są końce obiektu i który przechodzi przez punkt wyznaczony przez „oko obserwatora” (należy tutaj przywołać znany fakt, że trzy niewspółliniowe punkty wyznaczaja w sposób jednoznaczny okrąg). Oczywiście łuk okręgu, który jest symetryczny do danego względem prostej $A B$ , jest zbiorem punktów o tej samej własności.

Problem 1

Zajmiemy się teraz konstrukcją miejsca geometrycznego punktów, z których dany odcinek $A B$ widać pod zadanym kątem $α$ .

R1PpdysLsWOr7

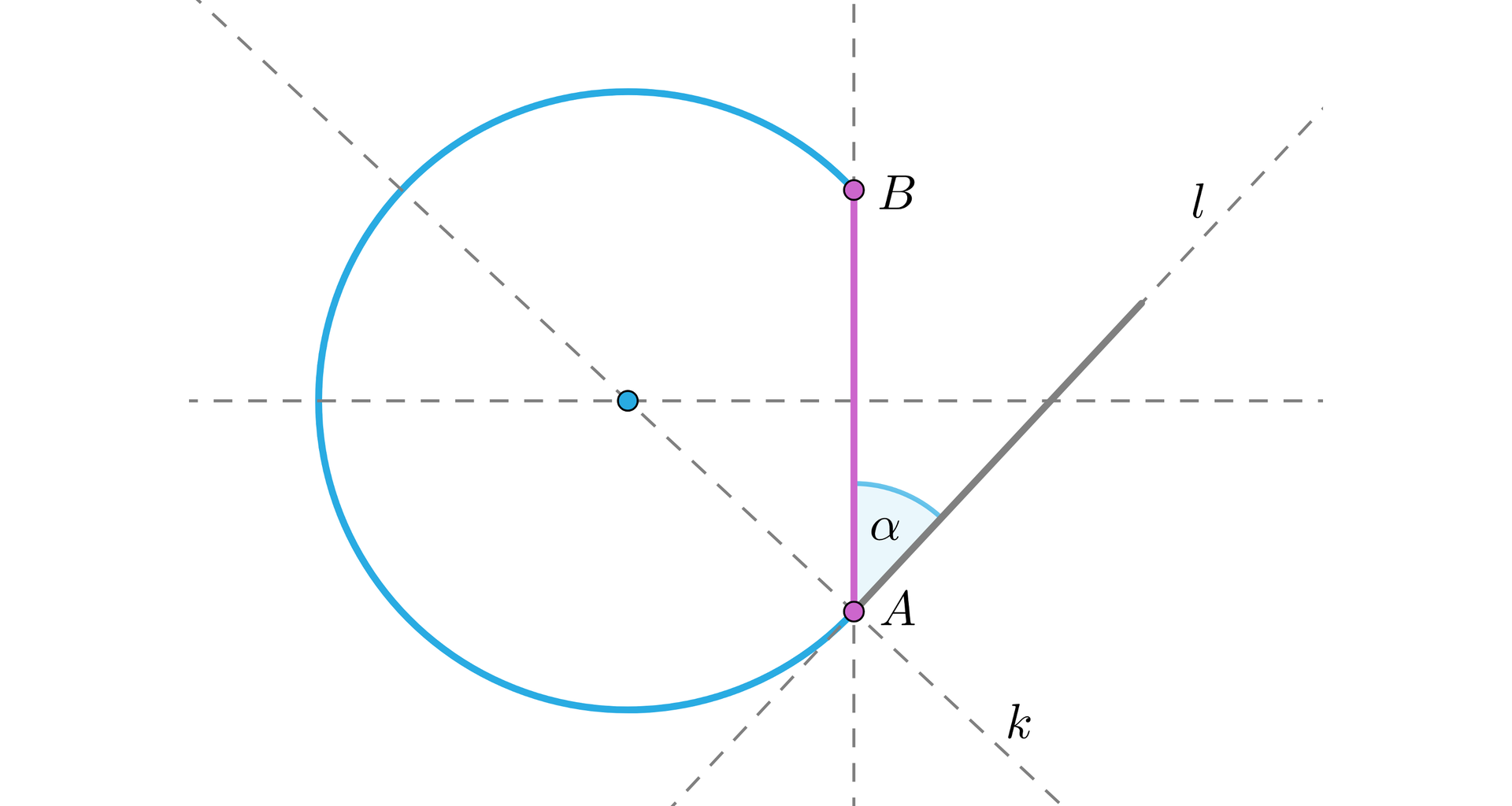
Grafika przedstawia część okręgu oraz odcinek AB. Punkty A oraz B leżą na okręgu po prawej stronie od środka okręgu, przy czym punkt A jest niżej od punktu B. Odcinek łączący punkt A z punktem B ma orientację pionową i kolor różowy. Odcinek ten leży na prostej która jest narysowana linią przerywaną. Środek okręgu jest zaznaczony punktem w Kolorze niebieskim. Przez środek okręgu przechodzą dwie linie. Obie linie są narysowane linią przerywaną. Jedna z nich ma orientację poziomą, a druga jest poprowadzona w taki sposób, że przechodzi przez punkt A. Prosta ta jest podpisana literą k. Przez punkt A przechodzi jeszcze prosta l, która jest styczna do okręgu i również jest narysowana linią przerywaną. Kąt pomiędzy odcinkiem AB a prostą l jest podpisany literą alfa. — Konstrukcja miejsca geometrycznego

Opis konstrukcji:

Na prostej odmierzamy odcinek $A B$ .
Odkładamy kąt $α$ w taki sposób, że wierzchołkiem kąta będzie punkt $A$ , a jedno ramię kąta zawiera dany odcinek – drugie ramię wyznacza prostą $l$ .
Kreślimy prostą prostopadłą do $l$ , przechodzącą przez punkt $A$ – otrzymujemy prostką $k$ .
Kreślimy symetralną odcinka $A B$ – punkt wspólny tej symetralnej i prostej $k$ wyznacza punkt $O$ .
Z punktu $O$ kreślimy łuk o końcach w punktach $A$ i $B$ .

Wykreśliliśmy tylko jedną z części szukanego zbioru. Pozostaje wyznaczyć teraz punkt symetryczny do punktu $O$ , względem odcinka $A B$ i nakreślić drugi – symetryczny łuk.

Dla dowodu poprawności konstrukcji poprowadzimy cięciwę wyznaczoną przez punkt $A$ i przez symetralną odcinka, oraz oznaczymy przez $S$ środek odcinka $A B$ , jak na rysunku.

R1M2U3sSvrjYC

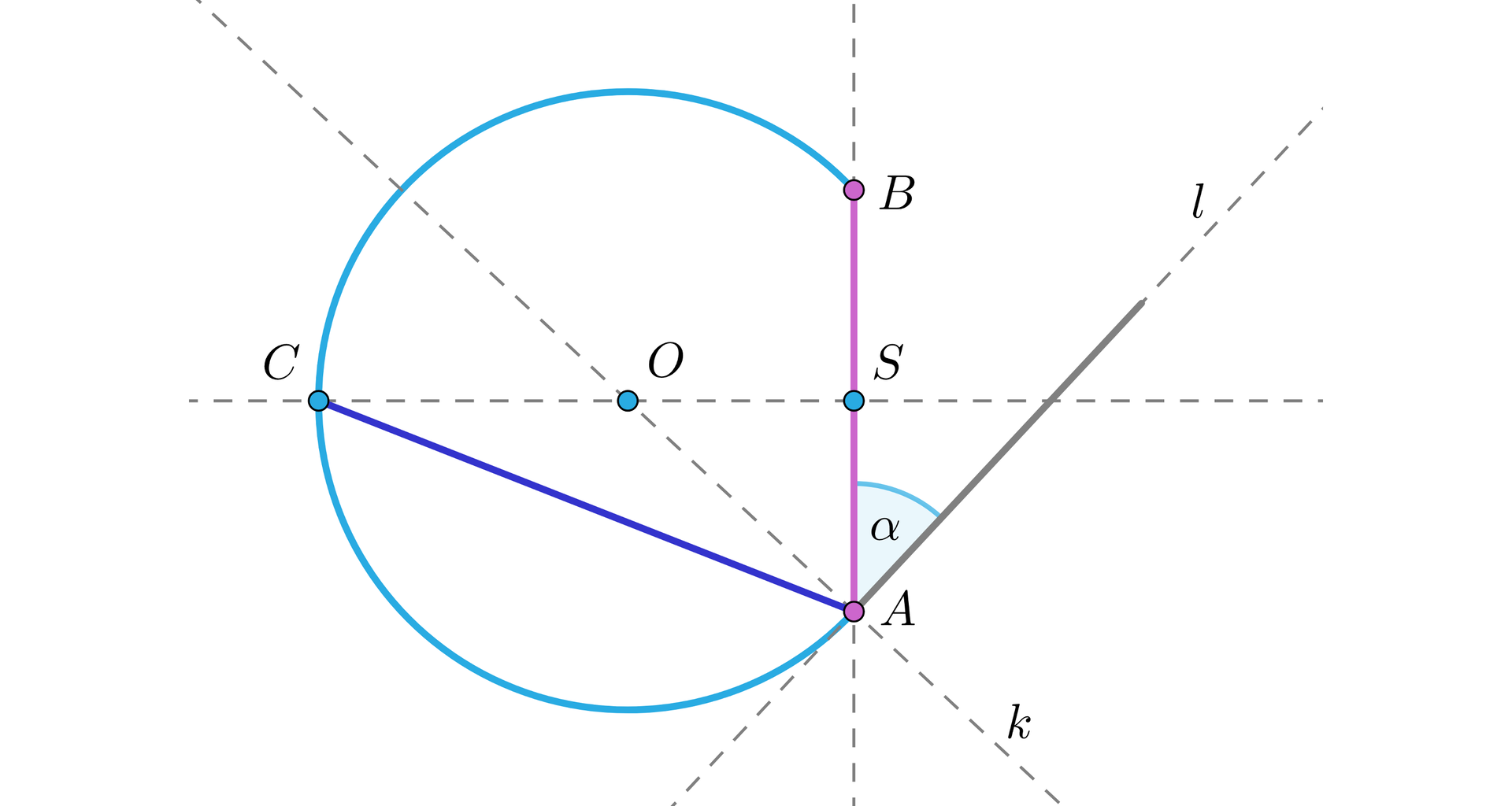
Grafika przedstawia część okręgu, odcinek AB oraz cięciwę AC . Punkty A oraz B leżą na okręgu po prawej stronie od środka okręgu, przy czym punkt A jest niżej od punktu B. Odcinek łączący punkt A z punktem B ma orientację pionową i kolor różowy. Odcinek ten leży na prostej która jest narysowana linią przerywaną. Środek okręgu jest zaznaczony punktem w kolorze niebieskim. Przez środek okręgu przechodzą dwie linie. Obie linie są narysowane linią przerywaną. Jedna z nich ma orientację poziomą i po lewej stronie na przecięciu z okręgiem wyznacza punkt C, natomiast po prawej stronie na przecięciu z odcinkiem AB wyznacza punkt S. Druga prosta przechodząca przez środek okręgu jest poprowadzona w taki sposób, że przechodzi przez punkt A. Prosta ta jest podpisana literą k. Przez punkt A przechodzi jeszcze prosta l, która jest styczna do okręgu i również jest narysowana linią przerywaną. Kąt pomiędzy odcinkiem AB a prostą l jest podpisany literą alfa. — Dowód poprawności konstrukcji

Zauważmy, że $|∡ O A B| = 90 ° - α$ oraz $|∡ A O S| = 90 ° - (90 ° - α) = α$ .

Kąt $A O S$ jest kątem zewnętrznym w trójkącie równoramiennym $A O C$ , zatem $α = |∡ A O S| = 2 \cdot |∡ A C O|$ .

Stąd $|∡ A C O| = \frac{α}{2}$ .

Symetralna jest osią symetrii trójkąta $A C B$ , zatem $|∡ A C B| = α$ .

Pozostaje jeszcze udowodnić, że tę własność ma każdy punkt leżący na wykreślonym łuku. Ale to już jest przedmiotem poniższego twierdzenia i wniosków, jakie z tego twierdzenia wynikają.

Twierdzenie o kącie środkowym i wpisanym

Twierdzenie: Twierdzenie o kącie środkowym i wpisanym

Kąt wpisany jest równy połowie kąta środkowego opartego na tym samym łuku.

Dowód

Rozważymy trzy różne przypadki, w zależności od położenia kąta wpisanego względem środka okręgu, które wyczerpują wszystkie wzajemne położenia środka okręgu i kąta wpisanego w tym okręgu.

Przypadek 1.

Przypuśćmy, że średnica okręgu zawiera się w jednym z ramion kąta wpisanego, jak na rysunku.

RLRH1YxCfZgZM

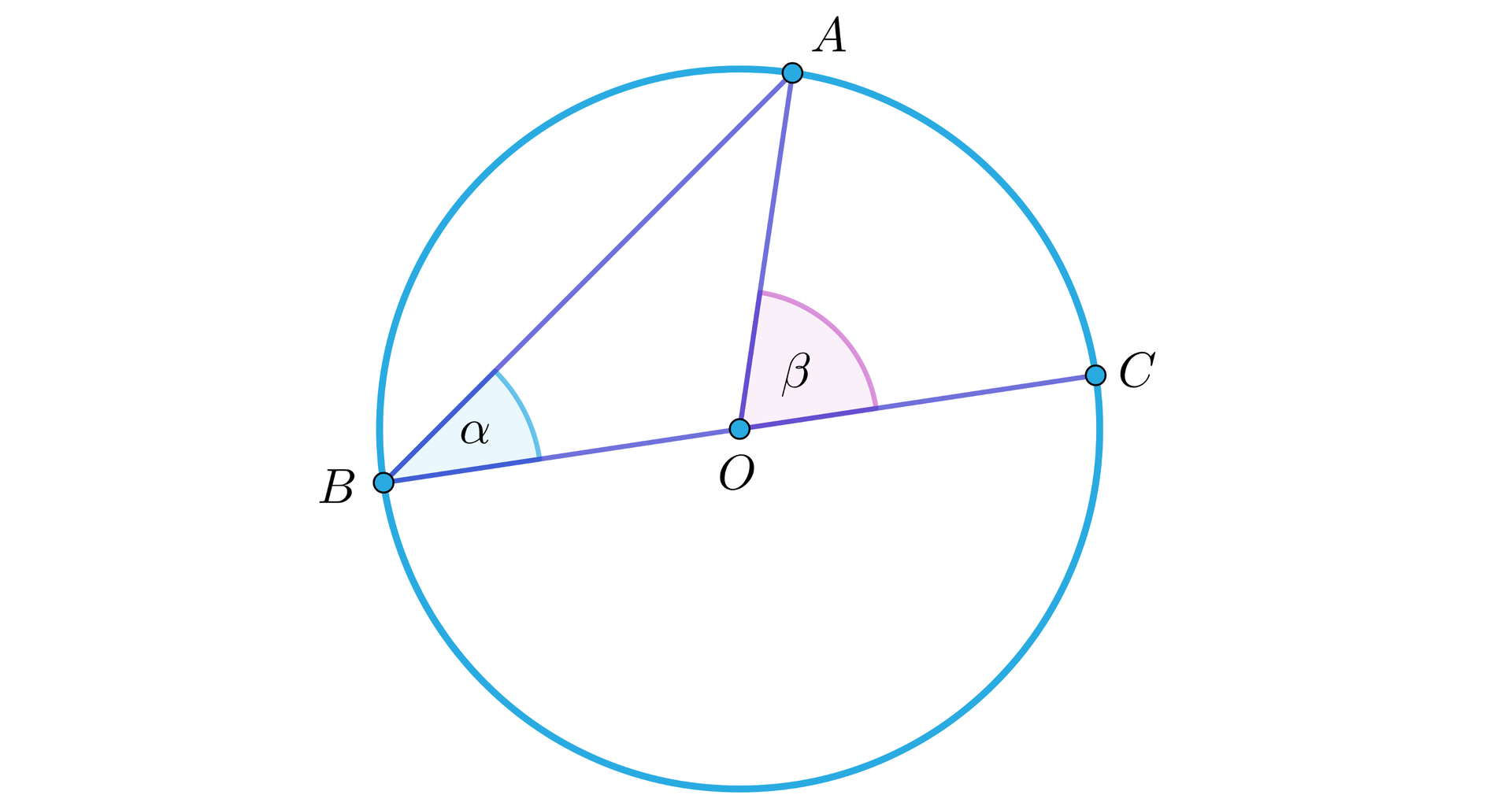
Grafika przedstawia okrąg, 4 punkty: A, B, C, O oraz łączące je odcinki. Środek okręgu jest oznaczony literą O. Punkty: A, B, C leżą na okręgu, w taki sposób, że punkty B, O, C leżą w jednej linii i tworzą średnicę okręgu. Kąt pomiędzy odcinkiem AB i odcinkiem BC jest podpisany literą alfa. Kąt pomiędzy odcinkiem AO a odcinkiem OC jest podpisany literą beta.

Kąt środkowy $β$ i kąt wpisany $α$ są oparte na łuku $A C$ .

Zauważmy, że $β$ jest kątem zewnętrznym w trójkącie równoramiennym $A O B$ , w którym $|∡ A B O| = |∡ B A O| = α$ .

Miara kąta zewnętrznego w trójkącie jest równa sumie miar dwóch kątów do niego nieprzyległych, czyli $β = 2 α$ , co należało wykazać.

Przypadek 2.

Przypuśćmy, że środek okręgu leży wewnątrz kąta wpisanego, jak na rysunku.

Re4tothRO1k8v

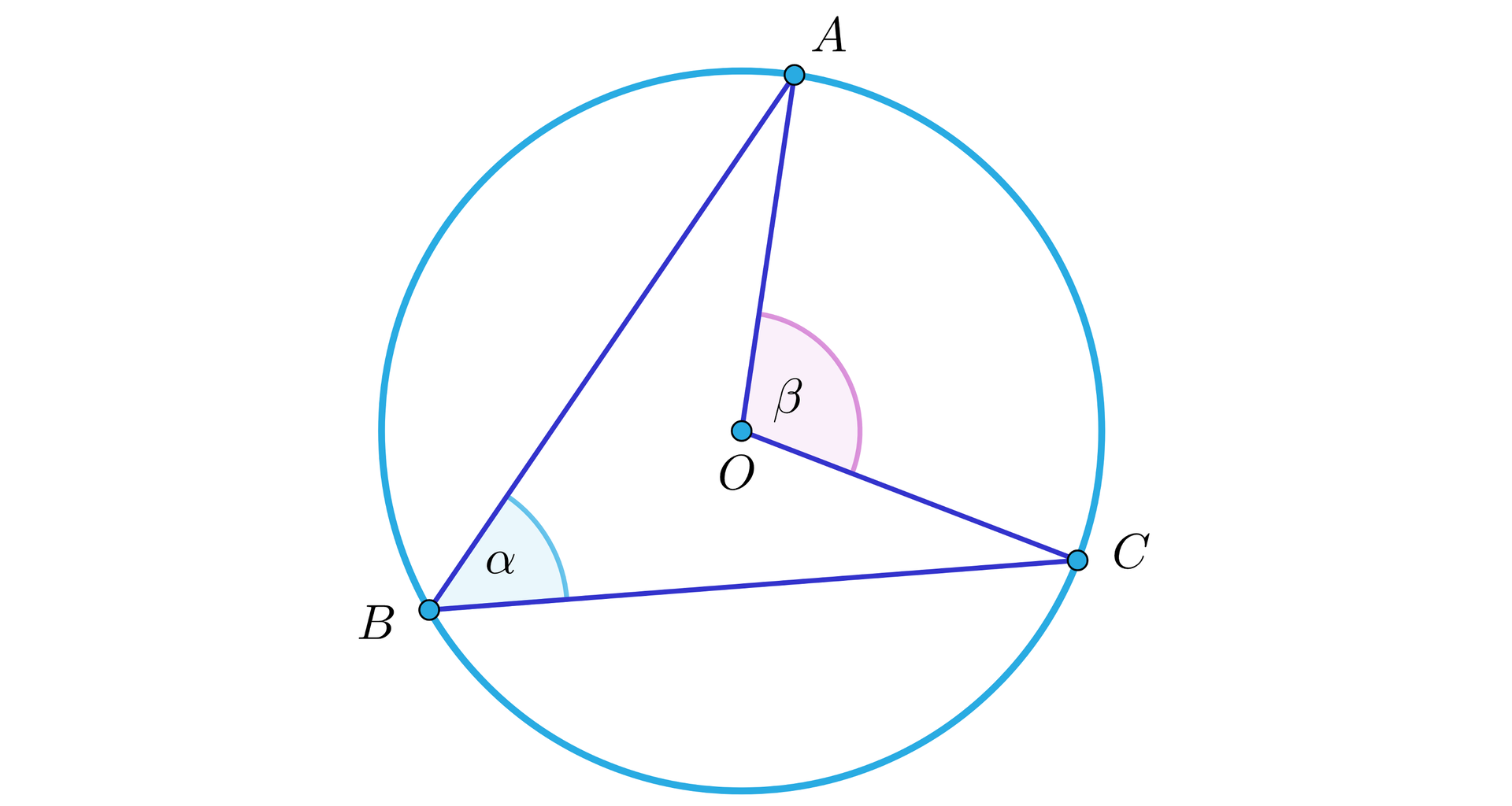
Kąt środkowy $β$ i kąt wpisany $α$ są oparte na łuku $A C$ .

Poprowadźmy średnicę o końcu w punkcie $B$ .

Dzieli ona kąty: wpisany i środkowy na kąty odpowiednio: $α_{1}$ , $α_{2}$ oraz $β_{1}$ , $β_{2}$ , jak na rysunku.

RbHnR6NECkdSX

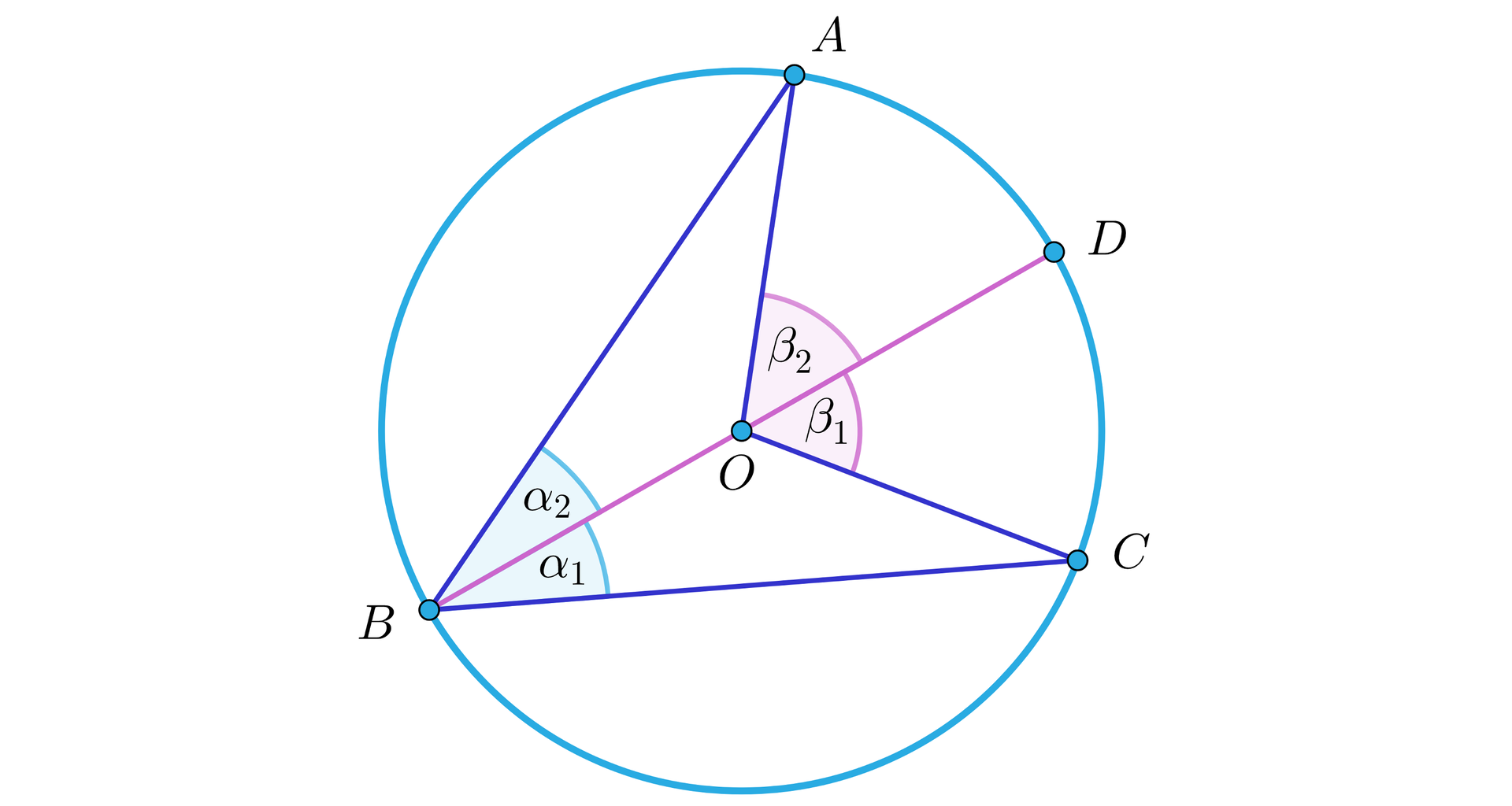
Grafika przedstawia okrąg, 5 punktów: A, B, C, D, O oraz łączące je odcinki. Środek okręgu jest oznaczony literą O. Punkty: A, B, C leżą na okręgu, w taki sposób, że punkty B, C leżą poniżej środka okręgu, natomiast punkt A znajduje się powyżej środka okręgu. Punkt D znajduje się na okręgu pomiędzy punktem A oraz C. Przez punkt B, O oraz poprowadzona jest średnica okręgu. Kąt pomiędzy odcinkiem BC i odcinkiem BD jest podpisany literą alfa dolny indeks 1. Kąt pomiędzy odcinkiem AB i odcinkiem BD jest podpisany literą alfa dolny indeks 2. Kąt pomiędzy odcinkiem CO a odcinkiem OD jest podpisany literą beta dolny indeks 1. Kąt pomiędzy odcinkiem AO a odcinkiem OD jest podpisany literą beta dolny indeks 2.

Zauważmy, że do kątów: wpisanego i środkowego, opartych na łuku $C D$ , możemy zastosować zależność udowodnioną już w Przypadku 1. Wtedy $β_{1} = 2 α_{1}$ .

Podobnie, do kątów: wpisanego i środkowego, opartych na łuku $A D$ , możemy zastosować udowodnioną już zależność. Wtedy $β_{2} = 2 α_{2}$ .

Ale $β = β_{1} + β_{2} = 2 α_{1} + 2 α_{2} = 2 \cdot (α_{1} + α_{2}) = 2 α$ , co należało wykazać.

Przypadek 3.

Pozostaje rozważyć sytuację, gdy środek okręgu leży na zewnątrz kąta wpisanego, jak na rysunku.

ROp9ozCk8hIcL

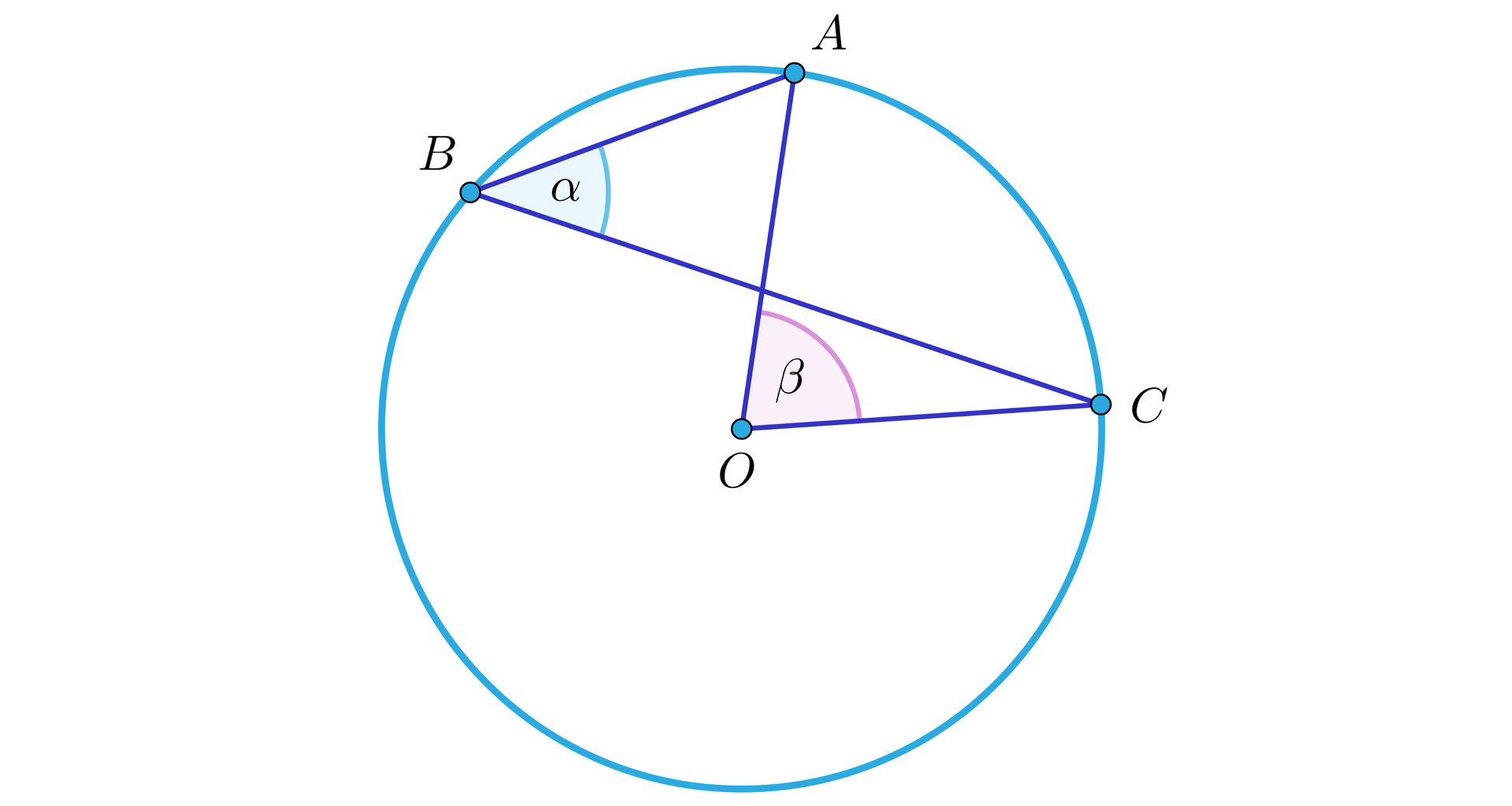
Kąt środkowy $β$ i kąt wpisany $α$ są oparte na łuku $A C$ .

Poprowadźmy średnicę o końcu w punkcie $B$ .

Tworzy ona z ramieniem $B C$ kąta wpisanego oraz z ramieniem $O C$ kąta środkowego odpowiednio kąty: wpisany $α_{1}$ oraz środkowy $β_{1}$ , jak na rysunku.

R10MVubwWhFpj

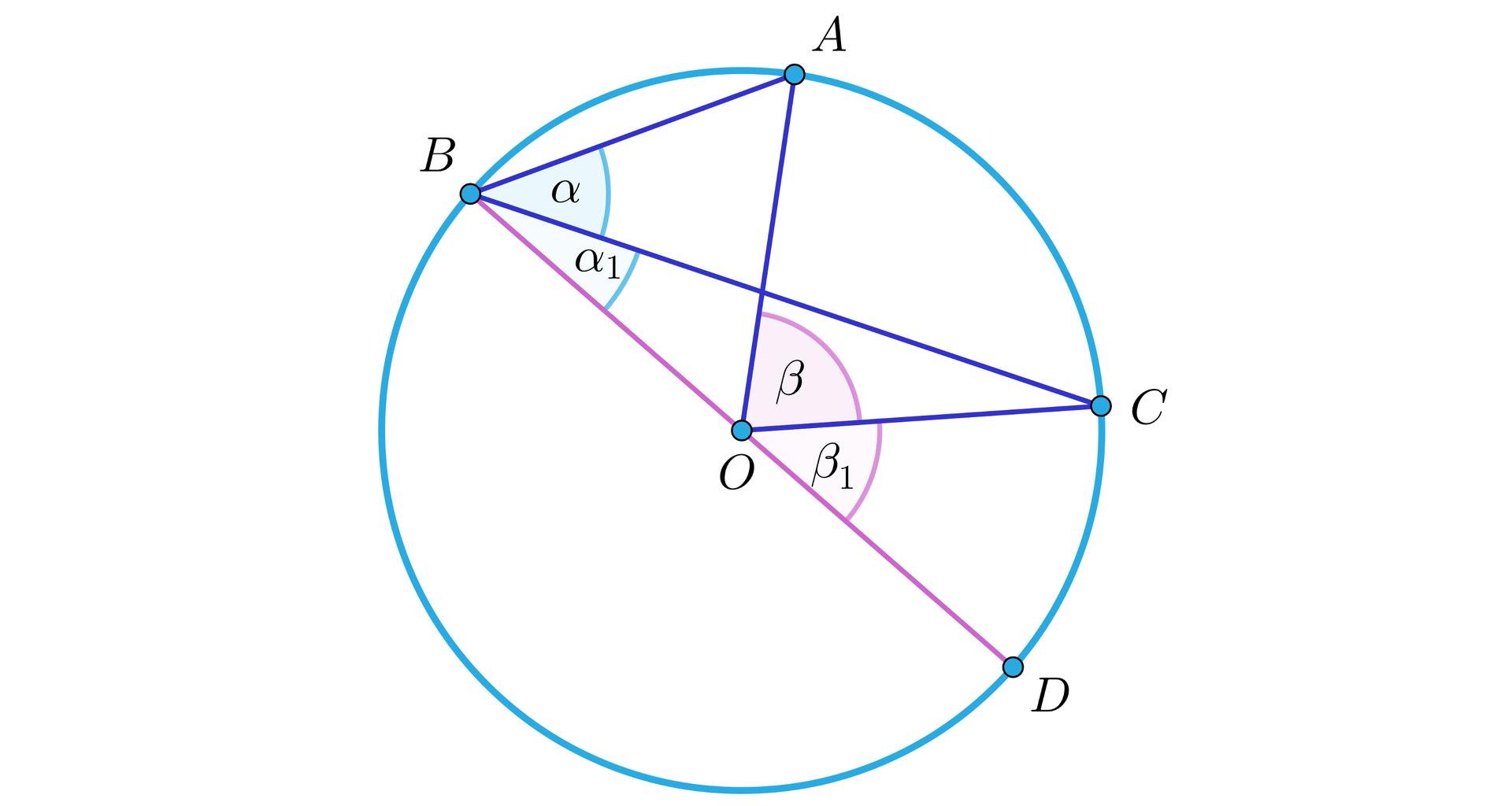
Zauważmy, że do kątów: wpisanego i środkowego, opartych na łuku $C D$ , możemy zastosować zależność udowodnioną już w Przypadku 1. Wtedy $β_{1} = 2 α_{1}$ .

Podobnie, do kątów: wpisanego i środkowego, opartych na łuku $A D$ , możemy zastosować zależność udowodnioną w Przypadku 1. Wtedy $β + β_{1} = 2 \cdot (α + α_{1})$ .

Ale $β = (β + β_{1}) - β_{1} = 2 \cdot (α + α_{1}) - 2 α_{1} = 2 α$ , co należało wykazać.

Prostym wnioskiem z tego twierdzenia jest twierdzenie Talesa o kącie wpisanym.

Twierdzenie Talesa o kącie wpisanym

Twierdzenie: Twierdzenie Talesa o kącie wpisanym

Kąt wpisany rozpięty na średnicy okręgu jest prosty, jako kąt dwa razy mniejszy od kąta półpełnego, czyli kąta środkowego rozpiętego na tej średnicy.

Pozostaje sformułować wniosek, który stanowi nie tylko uzupełnienie dowodu poprawności wcześniejszej konstrukcji, ale jest ważnym narzędziem w rozwiązywaniu zadań z planimetrii.

Twierdzenie o kątach wpisanych

Twierdzenie: Twierdzenie o kątach wpisanych

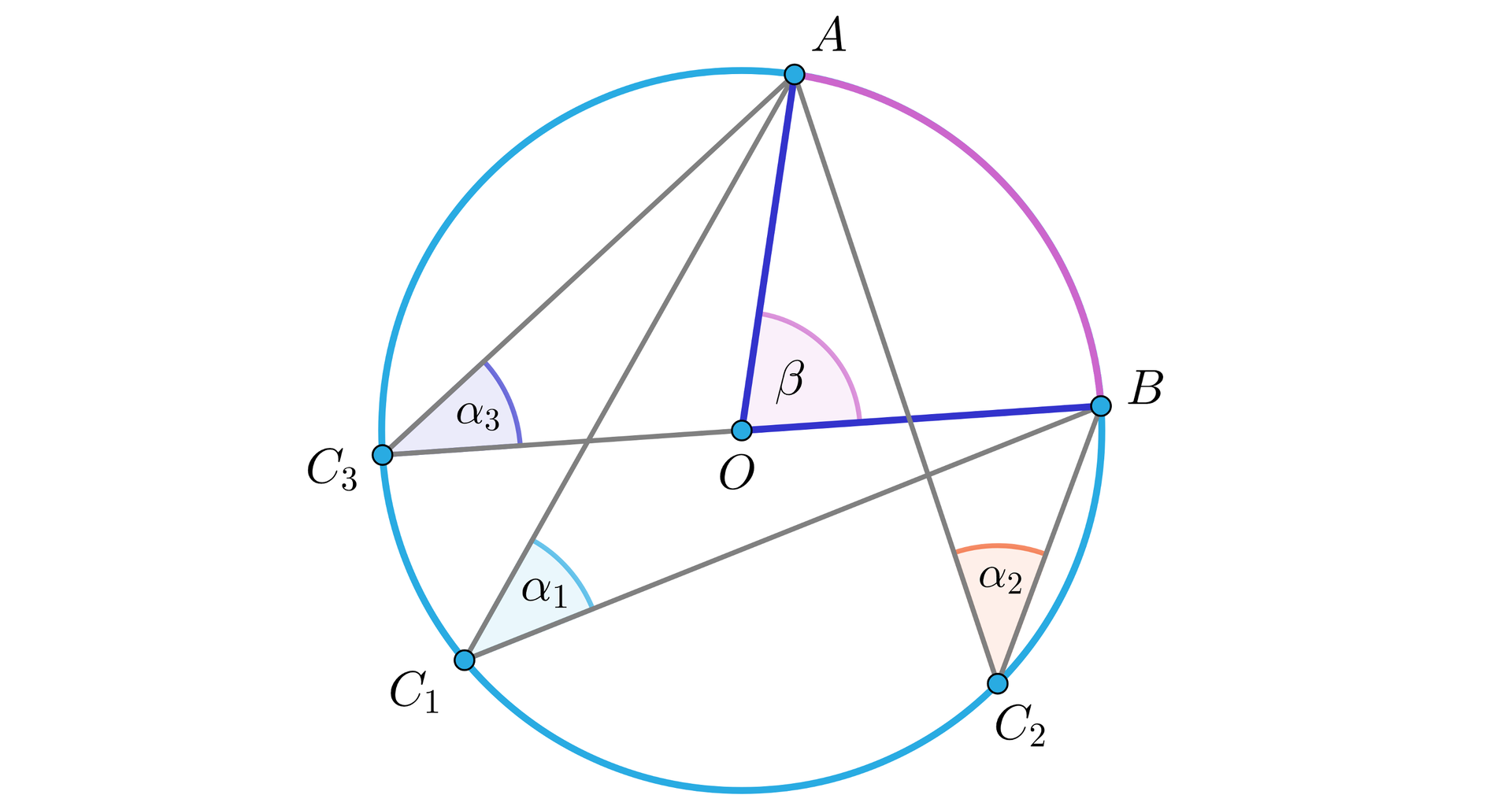
Wszystkie kąty wpisane oparte na tym samym łuku mają równe miary.

Dowód

Zauważmy, że dany łuk $A B$ jednoznacznie wyznacza kąt środkowy. Z kolei istnieje wiele kątów wpisanych opartych na tym samym łuku, ale miara każdego z tych kątów jest dwa razy mniejsza od miary kąta środkowego, tym samym te miary są sobie równe (patrz rysunek).

R11g2r0OOqkLU

Grafika przedstawia okrąg, 6 punktów: A, B, C dolny indeks 1, C dolny indeks 2, C dolny indeks 3, O oraz łączące je odcinki. Środek okręgu jest oznaczony literą O. Pozostałe punkty leżą na okręgu. Część okręgu pomiędzy punktem A i punktem B jest zaznaczona na kolor fioletowy. Kąt pomiędzy odcinkami AO i OB jest zaznaczony literą beta. Kąt pomiędzy odcinkami: C dolny indeks 1,A oraz C dolny indeks 1, B jest podpisany literą alfa dolny indeks 1. Kąt pomiędzy odcinkami: C dolny indeks 2,A oraz C dolny indeks 2, B jest podpisany literą alfa dolny indeks 2. Kąt pomiędzy odcinkami: C dolny indeks 3,A oraz C dolny indeks 3, B jest podpisany literą alfa dolny indeks 3.

Twierdzenie o kątach wpisanych w okrąg

Twierdzenie: Twierdzenie o kątach wpisanych w okrąg

Kąty wpisane w dany okrąg, oparte na dwóch łukach o równej długości, są sobie równe.

Dowód

Popatrzmy na rysunek.

R1QhDbLZkvmmH

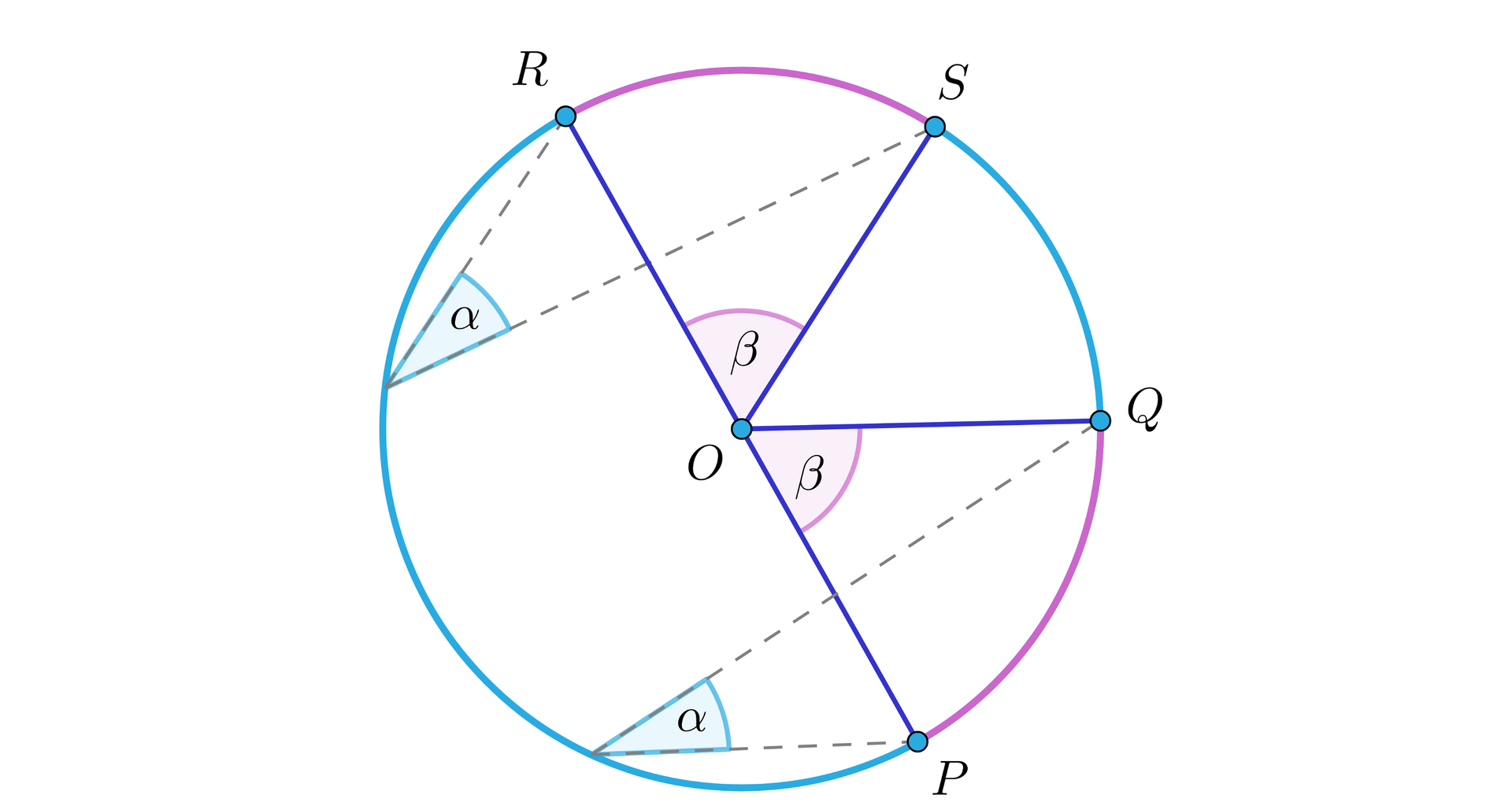
Grafika przedstawia okrąg. Środek okręgu jest zaznaczony literą O. Na okręgu znajdują się punkty: R, S, Q, P. Przy czym punkty fragment okręgu pomiędzy punktami R i S ma kolor fioletowy, oraz fragment okręgu znajdujący się pomiędzy punktami Q i P również ma kolor fioletowy. Punkty wyznaczają następujące odcinki: RO, SO, QO oraz PO. Kąt pomiędzy odcinkami RO i SO jest podpisany literą beta. Kąt pomiędzy odcinkami QO i PO jest również podpisany literą beta. Wewnątrz okręgu zaznaczone zostały jeszcze dwa kąty, w taki sposób, że wierzchołki tych kątów leżą na okręgu, kąty te popisane są literą alfa. Ramiona pierwszego kąta alfa są wyznaczone przez wierzchołek, znajdujący się na okręgu oraz punkt R oraz punkt S. Ramiona drugiego kąta alfa są wyznaczone przez wierzchołek znajdujący się na okręgu oraz punkt Q i punkt P. — Kąty oparte na równych łukach

Rozważmy łuki $P Q$ i $R S$ o równej długości.

Wtedy kąty środkowe oparte na tych łukach mają taką samą miarę – oznaczmy ją $β$ .

Ale każdy z kątów wpisanych opartych odpowiednio na łukach $P Q$ i $R S$ jest połową kąta środkowego, czyli ma miarę $α = \frac{β}{2}$ , co należało wykazać.

Przykład 1

Pokażemy zastosowanie twierdzenia o kącie wpisanym i środkowym w okręgu. Przyjmijmy, że na okręgu wyznaczono łuki $A B$ i $B C$ . Kąty środkowe oparte na tych łukach mają odpowiednio miary $50 °$ i $70 °$ . Wyznaczymy miary kątów trójkąta $A B C$ .

Popatrzmy na rysunek ilustrujący dane z zadania.

R1eJZtbXt9iJF

Grafika przedstawia okrąg. Środek okręgu jest zaznaczony literą O. Na okręgu znajdują się punkty: A, B, C, które tworzą trójkąt w kolorze różowym. Odcinki AO, BO oraz CO są zaznaczone linią przerywaną. Kąt pomiędzy odcinkiem AO a odcinkiem BO ma wartość 50 stopni. Kąt pomiędzy odcinkiem CO a odcinkiem BO ma wartość 70 stopni.

Dwa spośród kątów trójkąta to kąty oparte odpowiednio na tych samych łukach, co dane kąty środkowe.

Zatem $|∡ A C B| = \frac{1}{2} \cdot 50 ° = 25 °$ oraz $|∡ B A C| = \frac{1}{2} \cdot 70 ° = 35 °$ .

Z bilansu kątów trójkąta wynika, że $|∡ A B C| = 180 ° - 35 ° - 25 ° = 120 °$ .

Oczywiście, trzeci z kątów trójkąta można też wyznaczyć, jako kąt wpisany oparty na tym łuku o końcach $A$ , $C$ do którego nie należy punkt $B$ – kąt środkowy oparty na tym łuku ma miarę $360 ° - 70 ° - 50 ° = 240 °$ , a kąt wpisany jest dwa razy mniejszy.

Słownik

rozmiar kątowy

rozmiar kątowy, inaczej odległość kątowa $θ$ , pomiędzy dwoma obiektami, to kąt, którego ramionami są promienie „wychodzące z oka obserwatora” i przechodzące przez te obiekty; miarą takiej odległości są stopnie i jego części: minuty i sekundy

Wprowadzenie

Aplet

Miejsce geometryczne punktów, z których dany odcinek widać pod stałym kątem

Słownik