O proporcjach odcinkowych w trójkącie

Rozważmy trójkąt $ABC$, w którym dwusieczna $d$ kąta wewnętrznego $BAC$ przecięła bok $BC$ w punkcie $D$, jak na rysunku.

RJBnSy8tpGoj4

Grafika przedstawia trójkąt. Wierzchołki trójkąta to: A, B, C. Na boku BC leży punkt D. Przez punkt A i D przechodzi prosta, jest ona podpisana literą d. Kąt pomiędzy bokiem AC i prostą d jest podpisany $\alpha$. Kąt pomiędzy bokiem AB i prostą d jest podpisany $\alpha$.

Okazuje się, że długości odcinków $BD$ i $CD$ są związane z długościami boków $AB$ i $AC$ danego trójkąta.

Oznaczmy: $\left|\sphericalangle BAD\right|=\left|\sphericalangle CAD\right|=\alpha$ oraz $\left|\sphericalangle ADB\right|=\delta$. Wtedy $\left|\sphericalangle ADC\right|={180}^{\circ }-\delta$.

Z twierdzenia sinusów dla trójkąta $ABD$ mamy:

$\frac{\left|BD\right|}{\sin \alpha }=\frac{\left|AB\right|}{\sin \delta }$, stąd $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\sin \alpha }{\sin \delta }$.

Podobnie, z twierdzenia sinusów dla trójkąta $ACD$ mamy:

$\frac{\left|CD\right|}{\sin \alpha }=\frac{\left|AC\right|}{\sin \left(180°-\delta \right)}$, stąd $\frac{\left|CD\right|}{\left|AC\right|}=\frac{\sin \alpha }{\sin \left(180°-\delta \right)}$.

Ale $\sin \left(180°-\delta \right)=\sin \delta$. Zatem $\frac{\left|CD\right|}{\left|AC\right|}=\frac{\sin \alpha }{\sin \delta }$.

Porównując otrzymane wyniki możemy zapisać równość:

$\frac{\left|BD\right|}{\left|AB\right|}=\frac{\sin \alpha }{\sin \delta }=\frac{\left|CD\right|}{\left|AC\right|}$, z której wynika, że $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AC\right|}$.

Przeprowadzone rozumowanie jest nie najprostszym dowodem twierdzenia znanego pod krótką nazwą „twierdzenia o dwusiecznej”, którego sformułowanie zapisano poniżej.

Twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie

Twierdzenie: Twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie

W trójkącie dwusieczna kąta wewnętrznego dzieli bok przeciwległy na odcinki proporcjonalne do boków przyległych.

Dowód

Przeprowadzimy teraz dowód korzystając z narzędzi bardziej elementarnych, niż twierdzenie sinusów.

W tym celu, poprowadzimy przez punkt $C$ prostą równoległą do dwusiecznej $d$ i oznaczymy przez $E$ punkt wspólny tej prostej i przedłużenia boku $AB$, jak na rysunku.

R1WkKoxYe9goI

Grafika przedstawia trójkąt. Wierzchołki trójkąta to: A, B, C. Na boku BC leży punkt D. Przez punkt A i D przechodzi półprosta, jest ona podpisana literą d. Pomiędzy bokiem AC i prostą d zaznaczony jest kąt, ma on kolor niebieski. Pomiędzy bokiem AB i prostą d również zaznaczony jest kąt, ma on kolor niebieski. Po lewej stronie trójkąta znajduje się punkt E. Z punktu E wychodzi prosta, która przechodzi przez punkt C. Przez punkt E przechodzi również półprosta, która swój koniec ma w punkcie A. Kąt znajdujący się przy punkcie E jest zaznaczony kolorem zielonym. Kąt pomiędzy bokiem AC i odcinkiem EC również jest zaznaczony kolorem zielonym.

Mamy oczywiście $\left|\sphericalangle BAD\right|=\left|\sphericalangle AEC\right|$ oraz $\left|\sphericalangle DAC\right|=\left|\sphericalangle ACE\right|$.

Ale $\left|\sphericalangle BAD\right|=\left|\sphericalangle DAC\right|=\alpha$. Stąd $\left|\sphericalangle AEC\right|=\left|\sphericalangle ACE\right|=\alpha$ i trójkąt $CAE$ jest trójkątem równoramiennym, w którym $\left|AC\right|=\left|AE\right|$.

Z twierdzenia Talesa wynika w szczególności, że $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AE\right|}$, ale $\left|AC\right|=\left|AE\right|$, zatem $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AC\right|}$.

Co kończy dowód.

Zapiszemy jeszcze inny dowód tego twierdzenia, odwołujący się do własności pola trójkąta: stosunek pól trójkątów o równych wysokościach równy jest stosunkowi długości podstaw tych trójkątów.

Trójkąty $ABD$ i $ACD$ mają wspólną wysokość poprowadzoną z wierzchołka $A$, zatem $\frac{P_{ABD}}{P_{ACD}}=\frac{\left|BD\right|}{\left|CD\right|}$.

Ale $P_{ABD}=\frac{1}{2}·\left|AD\right|·\left|AB\right|·\sin \alpha$ oraz $P_{ACD}=\frac{1}{2}·\left|AD\right|·\left|AC\right|·\sin \alpha$, czyli $\frac{P_{ABD}}{P_{ACD}}=\frac{\frac{1}{2}·\left|AD\right|·\left|AB\right|·\sin \alpha }{\frac{1}{2}·\left|AD\right|·\left|AC\right|·\sin \alpha }=\frac{\left|AB\right|}{\left|AC\right|}$.

Stąd $\frac{\left|BD\right|}{\left|CD\right|}=\frac{P_{ABD}}{P_{ACD}}=\frac{\left|AB\right|}{\left|AC\right|}$, czyli $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AC\right|}$, co było do wykazania.

Rozważania podane niżej pokazują, że używanie skrótu myślowego o brzmieniu „twierdzenie o dwusiecznej” może być mylące, bowiem analogiczną proporcję zapiszemy w przypadku dwusiecznej kąta zewnętrznego.

Twierdzenie o dwusiecznej kąta zewnętrznego w trójkącie

Twierdzenie: Twierdzenie o dwusiecznej kąta zewnętrznego w trójkącie

Przypuśćmy, że w trójkącie $ABC$ dwusieczna kąta zewnętrznego przy wierzchołku $A$ przecina przedłużenie boku $BC$ w punkcie $D$. Wtedy odcinki $BD$ i $CD$ są proporcjonalne do odcinków $AB$ i $AC$, czyli

$\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AC\right|}$

R1CxyRYJLbZ1N

Grafika przedstawia trójkąt. Wierzchołki trójkąta to: A, B, C. Bok AB oraz BC zostały przedłużone w lewą stronę. Po lewej stronie na przedłużeniu boku BC znajduje się punkt D. Półprosta wychodząca z wierzchołka A i przechodząca przez punkt D jest podpisana literą d. Kąt pomiędzy bokiem AC i półprostą d jest podpisany literą delta. Kąt pomiędzy przedłużeniem boku AB i półprostą d jest podpisany literą delta.

Dowód

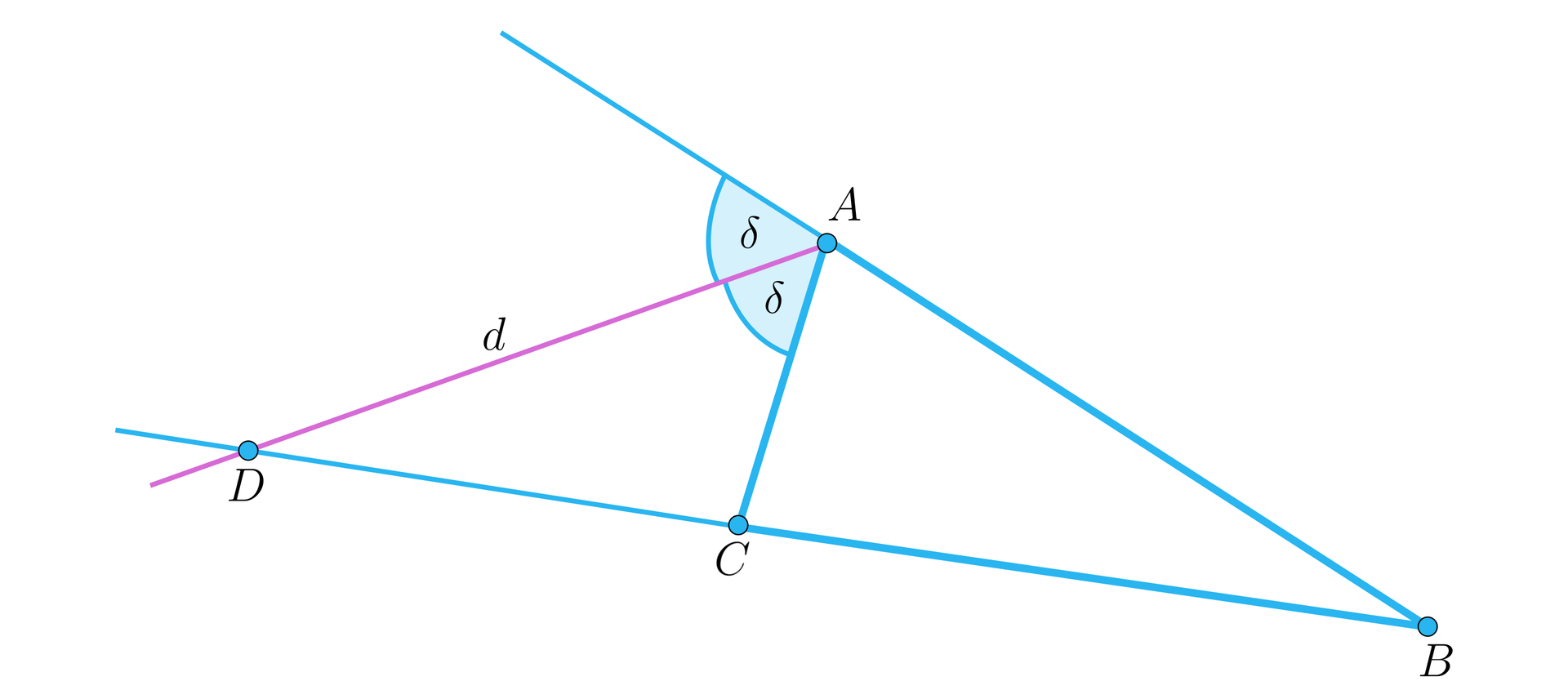
Zanim przeprowadzimy dowód, zauważmy, że niezbędne jest zapisanie, że dwusieczna przecina odpowiednie przedłużenie boku, bowiem gdybyśmy rozważyli trójkąt równoramienny $ABC$, w którym $\left|AB\right|=\left|AC\right|$, to wtedy dwusieczna kąta zewnętrznego przy wierzchołku $A$ byłaby równoległa do podstawy $BC$ tego trójkąta.

Przejdźmy teraz do dowodu i oznaczmy przez $\delta$ każdy z kątów, na jaki dwusiecznadwusiecznadwusieczna podzieliła kąt zewnętrzny przy wierzchołku $A$ oraz poprowadźmy równoległą do tej dwusiecznej, przechodzącą przez punkt $C$ i przecinającą bok $AB$ w punkcie $E$, jak na rysunku.

R1CmJFThexbK0

Grafika przedstawia trójkąt. Wierzchołki trójkąta to: A, B, C. Bok AB oraz BC zostały przedłużone do góry, przy czym przedłużenie boku BC wykonano linią przerywaną, a przedłużenie boku Ab zieloną linią ciągłą. Na przedłużeniu boku BC znajduje się punkt D. Prosta przechodząca przez wierzchołek A i punkt D jest podpisana literą d. Kąt pomiędzy bokiem AC i prostą d jest podpisany literą delta. Kąt pomiędzy przedłużeniem boku AB i prostą d jest podpisany literą delta. Linią przerywaną równolegle do prostej d poprowadzono prostą przez punkt C, punkt przecięcia się tej prostej z bokiem AB zaznaczono literą E.

Mamy oczywiście $\left|\sphericalangle ECA\right|=\left|\sphericalangle CAD\right|=\delta$ oraz $\left|\sphericalangle CEA\right|=\delta$.

Stąd trójkąt $CAE$ jest trójkątem równoramiennym, w którym $\left|AC\right|=\left|AE\right|$.

Z twierdzenia Talesa wynika w szczególności, że $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AE\right|}$, ale $\left|AC\right|=\left|AE\right|$, zatem $\frac{\left|BD\right|}{\left|AB\right|}=\frac{\left|CD\right|}{\left|AC\right|}$.

Co kończy dowód.

Słownik