Rozważmy proste o równaniach:

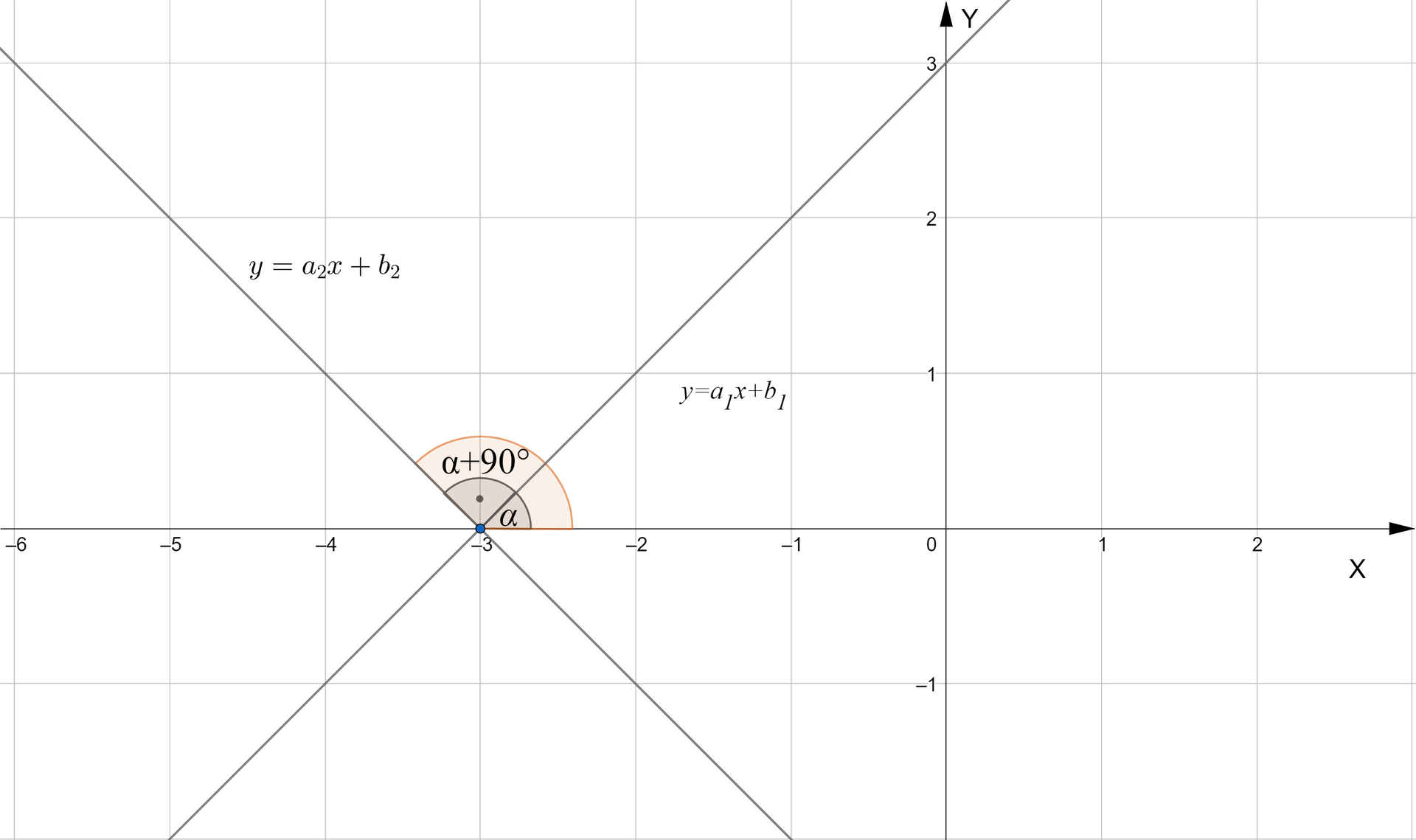
Przyjmijmy założenia jak na rysunku poniżej. Załóżmy, że są one prostopadłe. Oznacza to, że kąty nachylenia tych prostych do osi $X$ różnią się o $90°$.

Przypomnijmy, że $a_1=\mathrm{tg}\alpha$ oraz $a_2=\mathrm{tg}(\alpha +90°)$. Korzystając z tożsamości trygonometrycznych, możemy wykonać poniżesz przekształcenia:

Wynika stąd

Ponieważ powyższe rozumowanie można odwrócić, mamy więc prawo sformułować następujący wniosek, zwany warunkiem prostopadłości prostych.

Proste o równaniach kierunkowych

są prostopadłe wtedy i tylko wtedy, gdy iloczyn współczynników kierunkowychwspółczynnik kierunkowy prostejwspółczynników kierunkowych tych prostych jest równy $(-1)$.

Rjxzt3g36n7w4

Rysunek przedstawia układ współrzędnych z poziomą osią $X$ od minus sześciu do dwóch oraz z pionową osią $Y$ od minus dwóch do trzech. Na płaszczyźnie narysowane są dwie prostopadłe do siebie proste opisane wzorami: pierwsza: $y=a_{1}x+b_1$ oraz druga: $y=a_{2}x+b_2$. Na rysunku zaznaczono także następujące kąty: kąt ostry $\alpha$, który jest kątem nachylenia pierwszej prostej do osi $X$, kąt prosty między obiema prostymi oraz kąt między osią $X$ i drugą prostą o mierze: $\alpha +90°$.

Przykład 1

Rozstrzygniemy, czy proste o podanych równaniach są prostopadłe.

a) $y=0,\left(3\right)x-6$ i $y=-3x+2$

Odczytajmy współczynniki kierunkowe tych prostych

Zauważmy, że liczba $0,\left(3\right)$ to $\frac{1}{3}$, zatem

Wynika stąd, że proste o równaniach $y=0,\left(3\right)x-6$ i $y=-3x+2$ są prostopadłe.

b) $y=\sqrt{3}x-2x+6$ i $y=\sqrt{3}x+2x+5$

Uporządkujmy podane równania:

Odczytajmy współczynniki kierunkowe tych prostych

Zatem $a_1·a_2=(\sqrt{3}-2)(\sqrt{3}+2)=3-4=-1$.

Wynika stąd, że proste o równaniach $y=\sqrt{3}x-2x+6$ i $y=\sqrt{3}x+2x+5$ są prostopadłe.

c) $y=\left({\log }_{2}3\right)x+4$ i $y=\left({\log }_3\frac{1}{2}\right)x+2$

Odczytajmy współczynniki kierunkowe tych prostych

Zauważmy, że

Zatem

Wynika stąd, że proste o równaniach $y=\left({\log }_{2}3\right)x+4$ i $y=\left({\log }_3\frac{1}{2}\right)x+2$ są prostopadłe.

Przykład 2

Wyznaczymy równanie prostej przechodzącej przez punkt $A$ o współrzędnych $(2\sqrt{3},-\sqrt{3})$ prostopadłej do prostej o równaniu $y=-x+8$.

Odczytajmy współczynnik kierunkowy podanej prostej:

Szukana prosta ma równanie postaci

gdzie

Zatem po podstawieniu do warunku prostopadłości $a_1=-1$, otrzymujemy $a_2=1$. Aby wyznaczyć $b_2$ podstawimy współrzędne punktu $A$ do równania $y=x+b_2$:

Zatem równanie szukanej prostej to $y=x-3\sqrt{3}$.

Przykład 3

Wyznaczymy wartość parametru $m$, dla którego proste o równaniach

są prostopadłe.

Zaczniemy od uporządkowania równań i odczytania współczynników kierunkowych.

Ponieważ proste opisane równaniami kierunkowymi są prostopadłe dokładnie wtedy, gdy iloczyn ich współczynników kierunkowych jest równy $(-\mathrm{1)}$, wystarczy więc rozwiązać równanie

Wobec powyższego jedyna wartość parametru $m$, dla której proste o równaniach $y=-x+3\sqrt{5}m$ i $y=2mx-\sqrt{5}x-19m$ są prostopadłe to $\frac{(\sqrt{5}+1)}{2}$.

Przykład 4

Prosta $k$ jest prostopadła do prostej $l$. Wiadomo, że przecinają się one w punkcie $A(4,12)$. Prosta $k$ przecina oś $X$ w punkcie $(1,0)$. Wyznacz równania tych prostych wiedząc, że żadna z nich nie jest równoległa do osi $Y$.

Ponieważ żadna z prostych nie jest równoległa do osi $Y$, każdą z nich można opisać równaniem postaci

Najpierw wyznaczymy równanie prostej $k$. Korzystając z faktu, że przechodzi ona przez punkty o współrzędnych $(4,12)$ i $(1,0)$, możemy zapisać układ równań:

Po odjęciu równań stronami, otrzymujemy równanie

Zatem prosta $k$ ma równanie

Ponieważ prosta $l$ jest prostopadła do prostej $k$, współczynnik kierunkowy jej równania można wyznaczyć z warunku

Aby wyznaczyć $b_2$, podstawimy współrzędne punktu $(4,12)$ do równania $y=-\frac{1}{4}x+b_2$:

Zatem równanie szukanej prostej to

Słownik