Ułamki zwykłe
Założenia projektu
Ze szkoły podstawowej znasz operacje na liczbach naturalnych i całkowitych oraz na ułamkach zwykłych i dziesiętnych. Teraz twoim zadaniem będzie przygotowanie aplikacji ułatwiającej zrozumienie młodszym uczniom pojęcie ułamka zwykłego. Przykładową aplikację znajdziesz w e‑podręczniku do matematyki dla szkoły podstawowej. Możesz także obejrzeć działanie aplikacji w Scratchu na poniższym filmie.
Film dostępny na portalu epodreczniki.pl
Film: Działanie aplikacji ułatwiającej zrozumienie pojęcia ułamka zwykłego
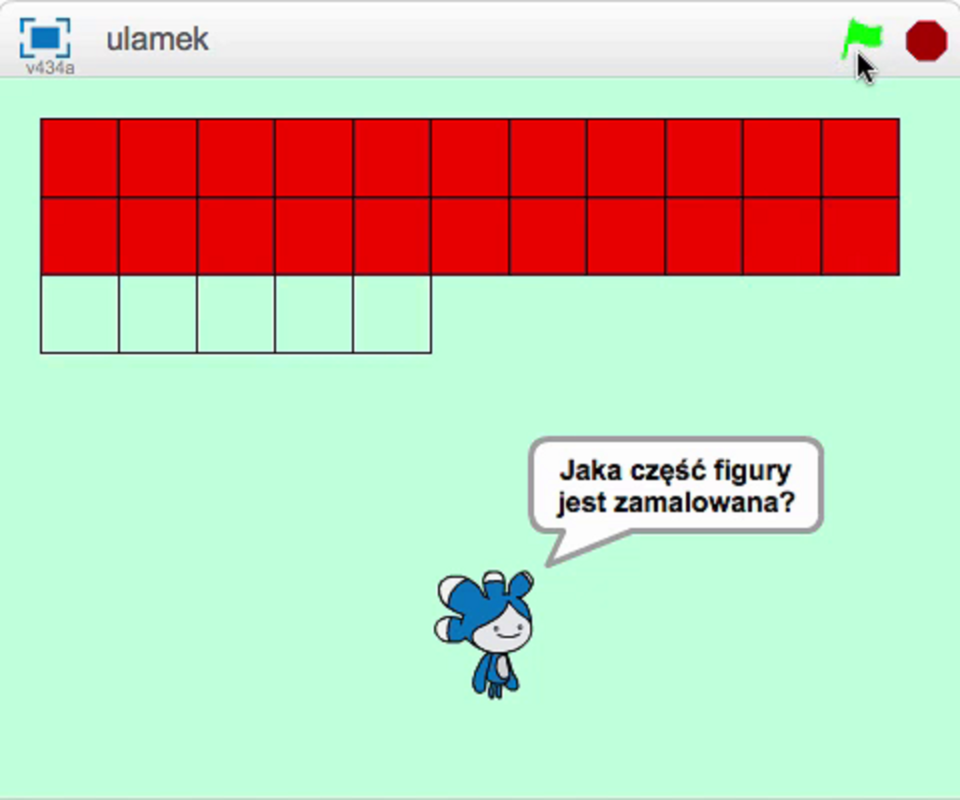
Na scenie duszek losuje licznik i mianownik ułamka oraz przedstawia go graficznie – w przykładowej aplikacji w postaci figury podzielonej na zamalowane i niezamalowane kwadraty (możesz zaproponować własną reprezentację graficzną ułamka, np. w postaci kawałków pizzy). Następnie prosi o podanie licznika i mianownika ułamka, czyli informacji, jaka część figury jest zamalowana. W kolejnym kroku sprawdza poprawność odpowiedzi.
Duszek przedstawia graficznie ułamek
Rozpocznij od rozplanowania sceny. Pamiętaj, że jej rozmiar to 480 na 360 pikseli.
Zastanów się, jaką przyjąć długość boku pojedynczego kwadratu, ile ich umieścić w jednym wierszu, ile maksymalnie wierszy zmieści się na scenie, aby zostało wolne miejsce dla duszka wyświetlającego komunikaty. Ustal na tej podstawie zakres losowania mianownika i licznika ułamka.
Zastanów się, w jaki sposób duszek narysuje (wyświetli) kwadraty na scenie. Skonsultuj swoje pomysły z kolegami i koleżankami. Spróbujcie zaproponować co najmniej dwa rozwiązania.
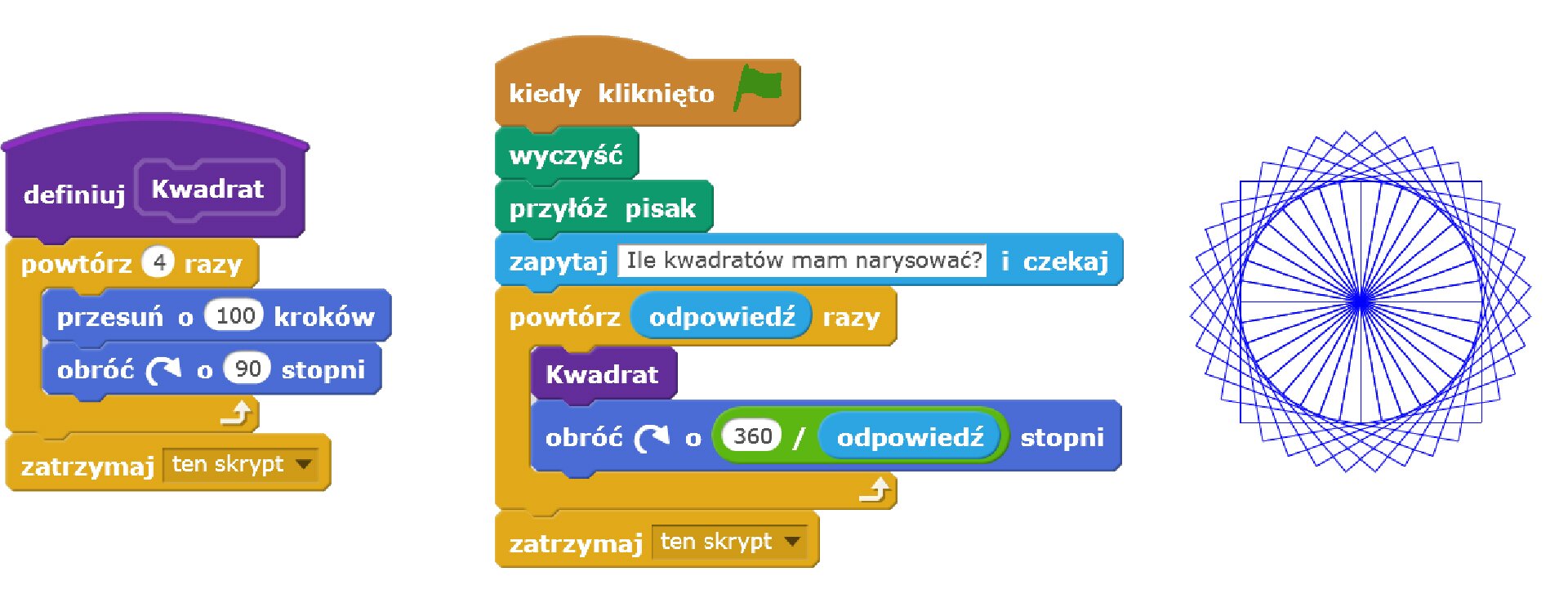
Duszek może rysować kwadraty. Nie powinno być problemów z narysowaniem niewypełnionego kwadratu. Jak poradzić sobie z zamalowanym kwadratem? Scratch dostarcza wielu poleceń do efektów graficznych, nie ma jednak polecenia do zamalowywania figur ani rysowania zamalowanych figur. Można narysować zamalowany kwadrat z odpowiedniej liczby odcinków, ale to rozwiązanie mało wygodne i powolne. Możesz też rysować odpowiednio pogrubionym pisakiem, ale końce tak rysowanego odcinka będą zaokrąglone, a więc nie będą to wtedy kwadraty.
Rozważ przygotowanie w edytorze graficznym dwóch kostiumów duszka w postaci zamalowanego i niezamalowanego kwadratu. Duszek może się ustawić w odpowiednim miejscu sceny i odcisnąć (przystemplować) swój kostium.
W edytorze graficznym przygotuj dwa kwadraty o długości boku np. 40, jeden zamalowany, drugi przezroczysty. Jeśli korzystasz z edytora graficznego Scratcha dodaj nowego duszka i narysuj jego dwa kostiumy. Jeśli z innego edytora, utwórz nowego duszka i wczytaj dwa kostiumy z plików graficznych. Pamiętaj, żeby sprawdzić punkt zaczepienia. Oba kostiumy powinny mieć go w tym samym punkcie, najlepiej w środku kwadratu lub w jego lewym górnym rogu.
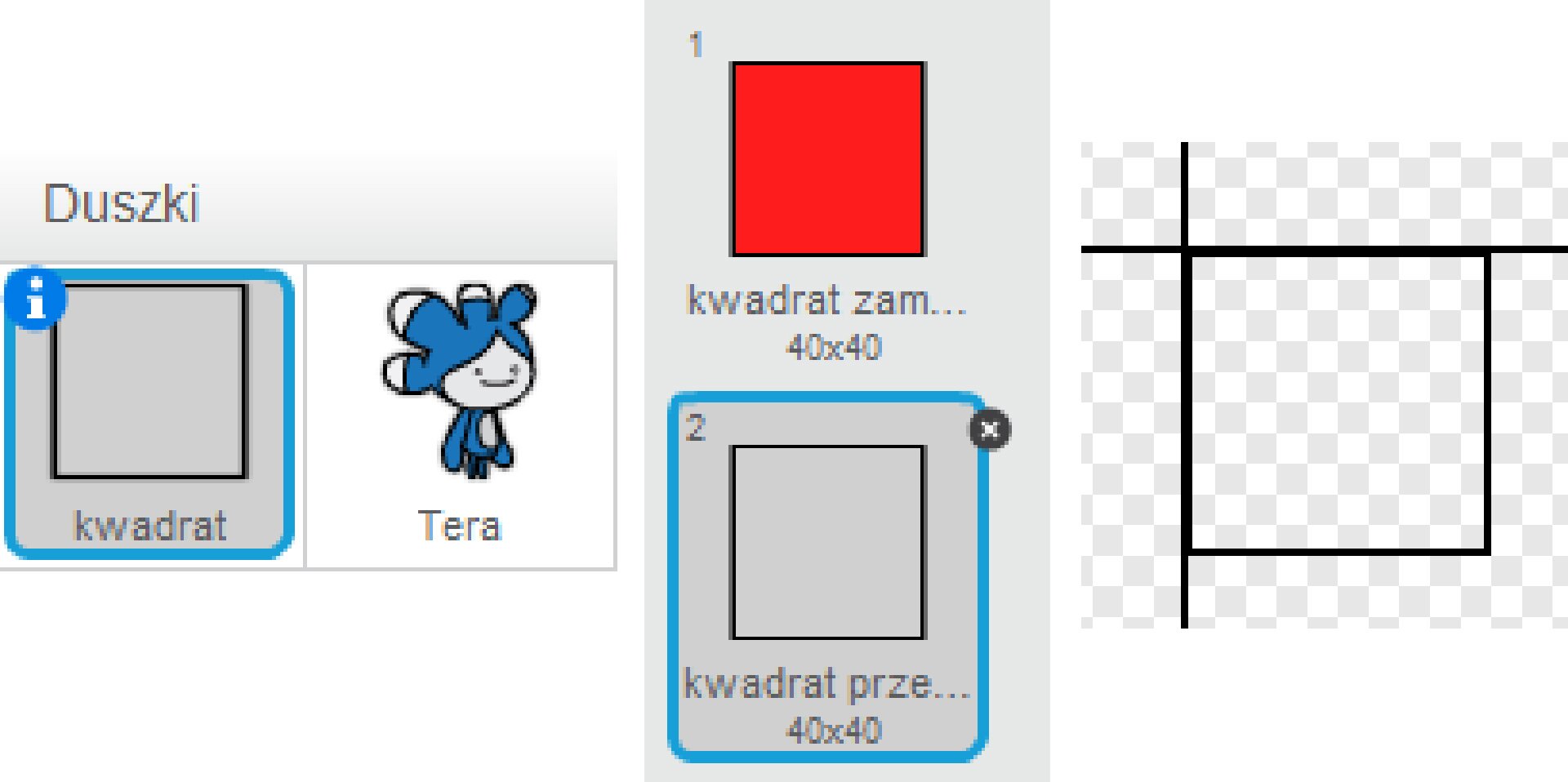
W projekcie będą więc występowały dwa duszki:
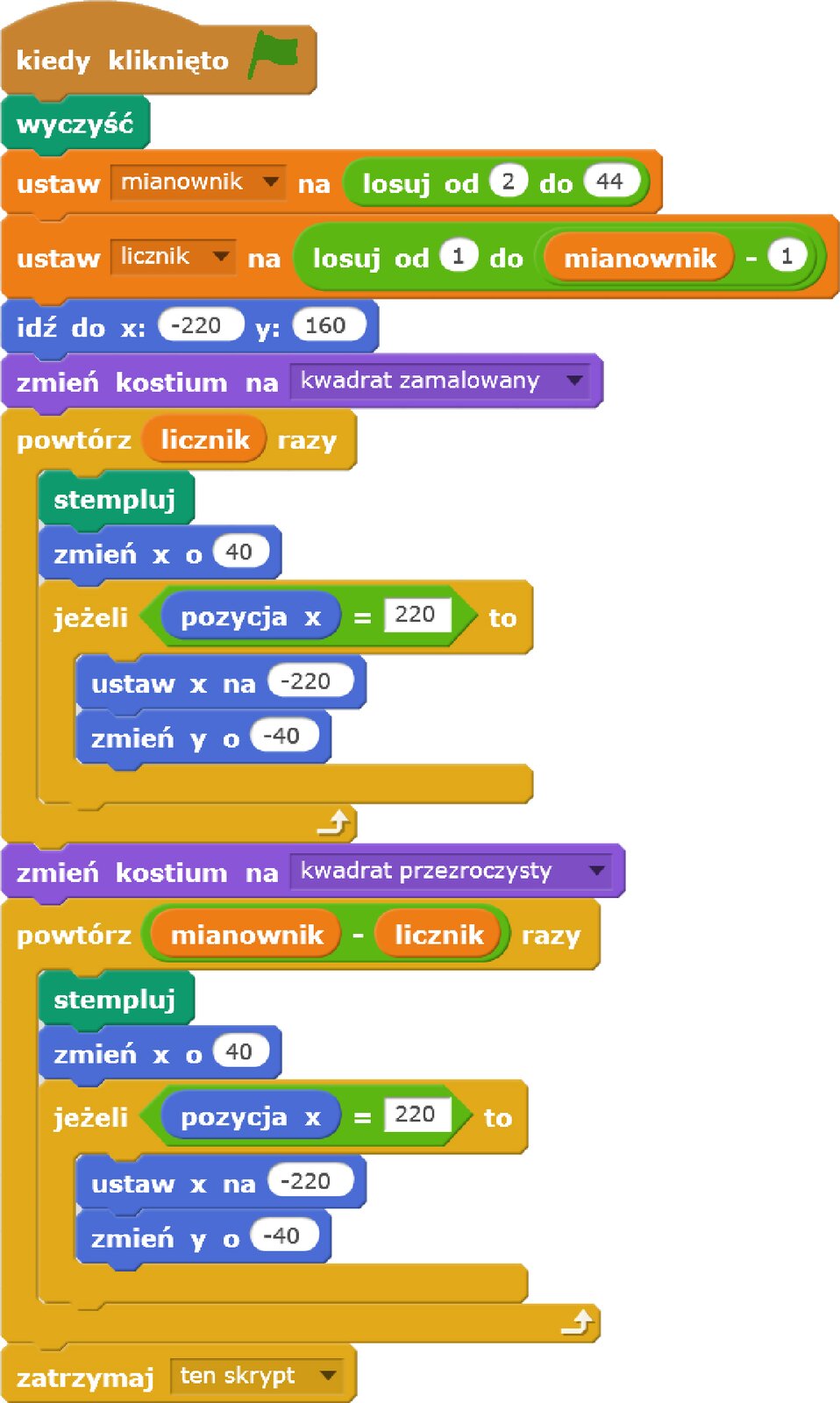
Ukryty duszek – kwadrat, którego zadaniem będzie (np. po kliknięciu w zieloną flagę) wylosowanie mianownika i licznika oraz przygotowanie zadania na scenie, czyli przystemplowanie odpowiedniej liczby kwadratów zgodnie z wylosowanymi wartościami.
Kotek (lub inna dowolnie przez ciebie wybrana postać), którego zadaniem będzie poproszenie o podanie odpowiedzi oraz sprawdzenie jej poprawności.
Wylosowany licznik i mianownik oraz podane wartości jako odpowiedzi będziesz musiał zapamiętać. Utwórz więc w projekcie cztery zmienne liczbowe (dostępne dla obu duszków) do przechowywania tych wartości.
Zapisz w punktach przypis postępowania (algorytm) dla duszka - kwadratu.
Zapisz skrypt realizujący algorytm z poprzedniego zadania. Następnie przetestuj działanie skryptu. Uruchom go kilkukrotnie, sprawdź, czy losują się różne ułamki.
Duszek sprawdza odpowiedź
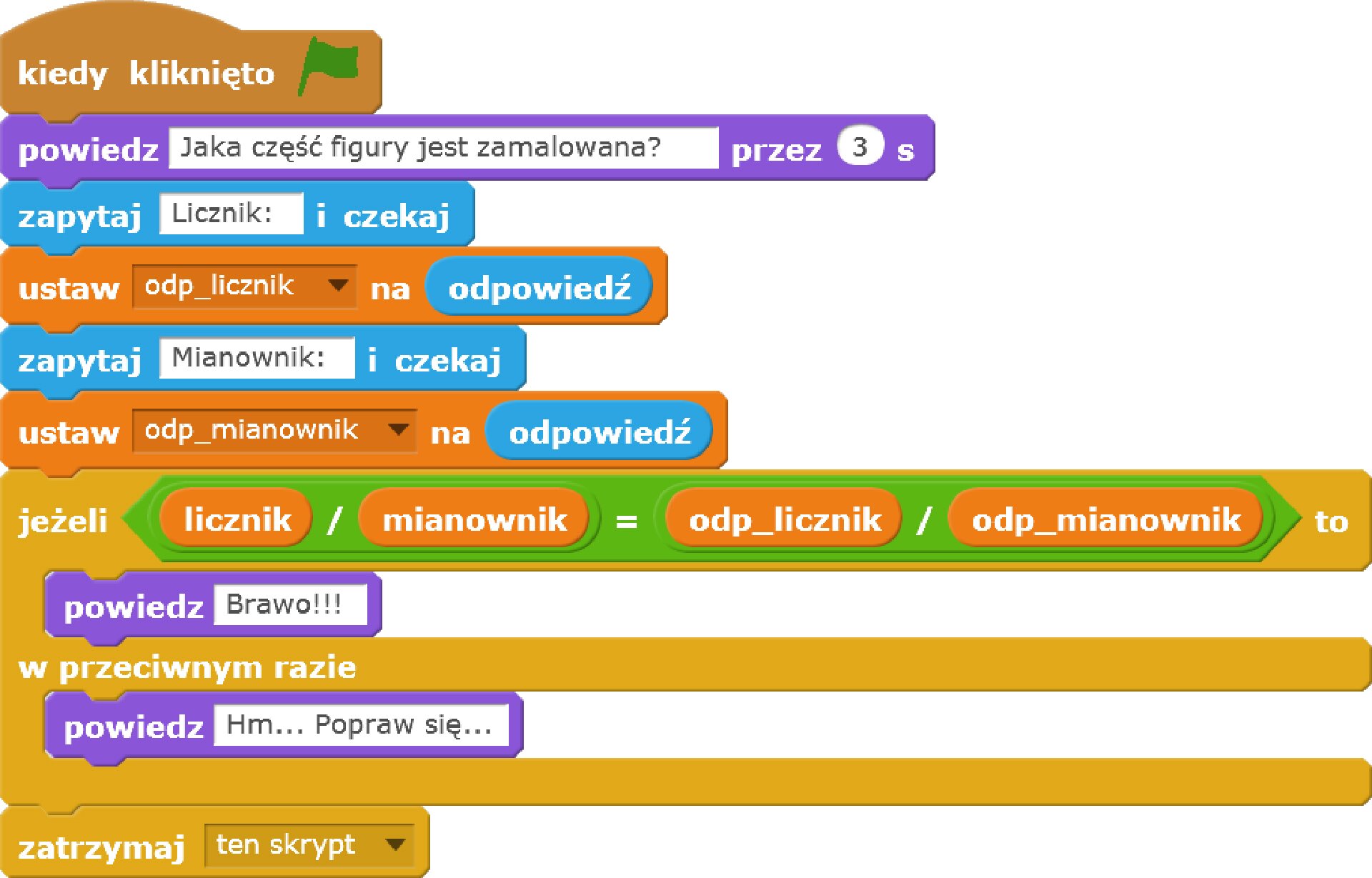
Zadania dla drugiego duszka są dużo prostsze. Powinien on poprosić o podanie odpowiedzi (licznik i mianownik ułamka określającego, jaka część figury jest zamalowana) oraz sprawdzić jej poprawność. Podane wartości wygodnie będzie zapamiętać w zmiennych, np. o nazwach odp_licznik i odp_mianownik.
Zastanów się, jak sprawdzić poprawność odpowiedzi. Czy porównanie wylosowanych wartości licznika i mianownika ułamka z wczytanymi wartościami wystarczy?
Spróbuj sformułować warunek logiczny, którego wynikiem będzie prawda także dla ułamka po redukcji (czyli po skróceniu).
Zapisz w punktach przypis postępowania (algorytm) dla duszka sprawdzającego odpowiedź.
Zapisz skrypt realizujący algorytm z poprzedniego zadania.
Przetestuj działanie projektu. Zastanów się, czy i jak można jeszcze poprawić sprawdzanie odpowiedzi. Czy uzasadnione jest wyświetlanie komunikatu „Brawo!”, kiedy grający poda prawidłowo wartość ułamka, ale go nie skróci? Może lepiej w takiej sytuacji wyświetlić komunikat np. „Dobrze, ale można skrócić ułamek...”. Czy potrafisz rozpoznać taki stan i poprawić skrypty?
Na kłopoty algorytmy – Euklides przychodzi z pomocą
Łatwo odpowiesz na pytanie, co trzeba zrobić, aby skrócić ułamek. Wystarczy znaleźć największą liczbę naturalną taką, która dzieli bez reszty zarówno licznik jak i mianownik ułamka, następnie podzielić licznik i mianownik przez ten dzielnik. Taką liczbę nazywamy największym wspólnym dzielnikiem i oznaczamy NWD.
Zastanów się i spróbuj zapisać algorytm znajdowania największego wspólnego dzielnika dwóch liczb. Twoje dane stanowią dwie liczby całkowite dodatnie, oznaczmy je przez a i b, natomiast wynikiem jest liczba całkowita dodatnia: NWD(a,b).
Wskazówka:
Do badania podzielności możesz wykorzystać operację arytmetyczną modulomodulo, czyli resztę z dzielenia dwóch liczb całkowitych.
Jeśli nie masz innych pomysłów, zauważ, że największy wspólny dzielnik nie może być większy od mniejszej z liczb a i b. Możesz więc rozpocząć od tej liczby i odejmować jedynkę tak długo, dopóki nie otrzymasz liczby, która dzieli bez reszty zarówno a, jak i b.
Wyszukaj informacje w internecie dotyczące Euklidesa, matematyka pochodzącego ze starożytnej Grecji, jego dzieła Elementy oraz algorytmu Euklidesa. Przygotuj krótką prezentację na ten temat.
Algorytm Euklidesa znajdowania największego wspólnego dzielnika dwóch liczb całkowitych dodatnich opiera się na następującej własności NWD:
NWD(a,b)=NWD(a‑b,b) przy założeniu, że a>b,
czyli, jeżeli większą liczbę zastąpimy różnicą większej i mniejszej, to wartość NWD się nie zmieni. Istotnie, jeśli k=NWD(a,b), to a=n*k i b=m*k, gdzie n i m to liczby całkowite dodatnie.
Wówczas a‑b=n*k‑m*k=(n‑m)*k, czyli k jest dzielnikiem różnicy a‑b.
Zastępując cyklicznie większą liczbę przez różnicę większej i mniejszej dojdziemy wcześniej lub później do sytuacji, że obydwie liczby są równe, w najgorszym przypadku obydwie będą równe 1. A dla dwóch takich samych liczb największy wspólny dzielnik jest im równy.
Przykład obliczenia NWD dla liczb 76 i 48, algorytmem Euklidesa na odejmowanie.

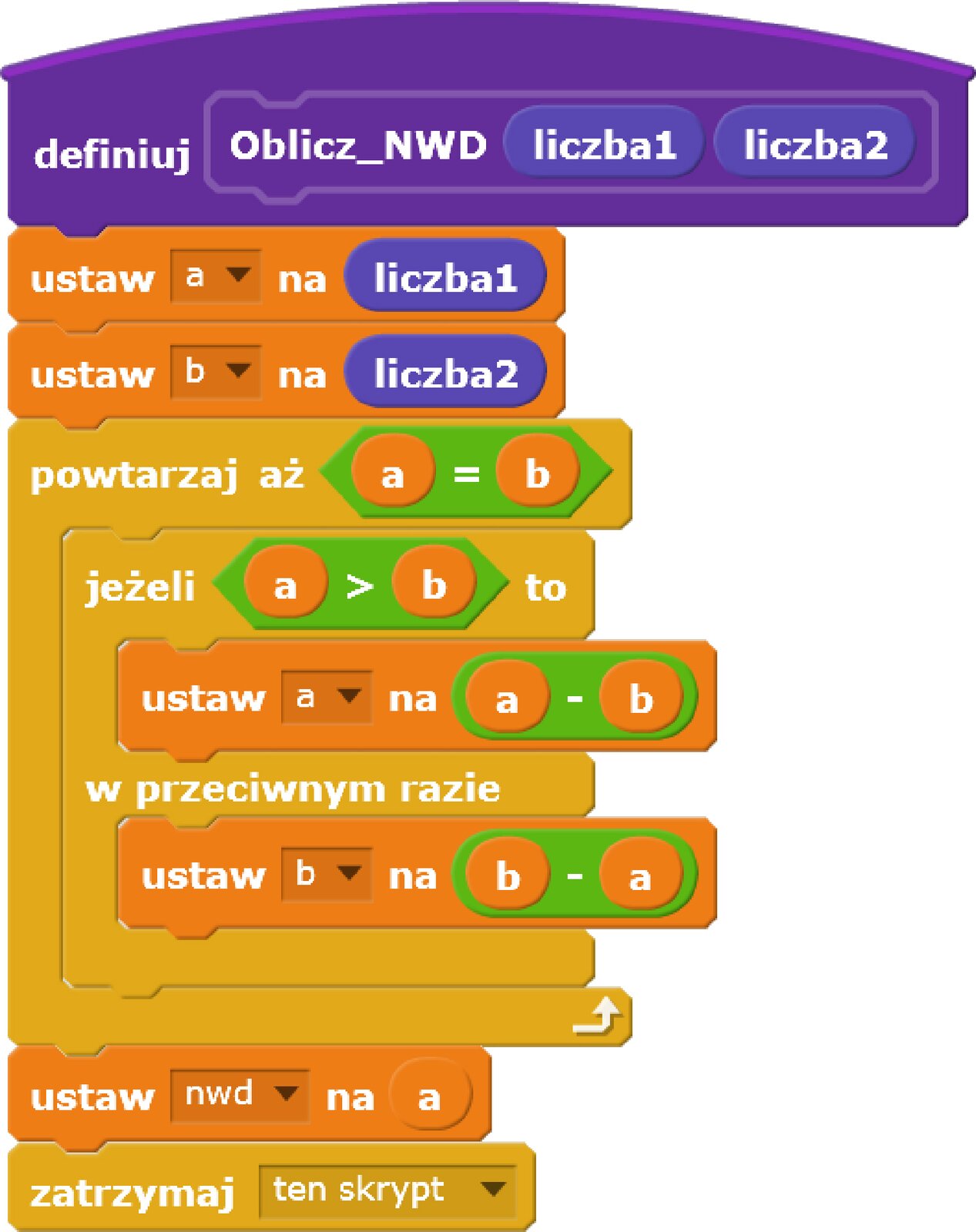
Zapisz w postaci listy kroków algorytm Euklidesa znajdowania największego wspólnego dzielnika dwóch liczb całkowitych dodatnich (z wykorzystaniem odejmowania).
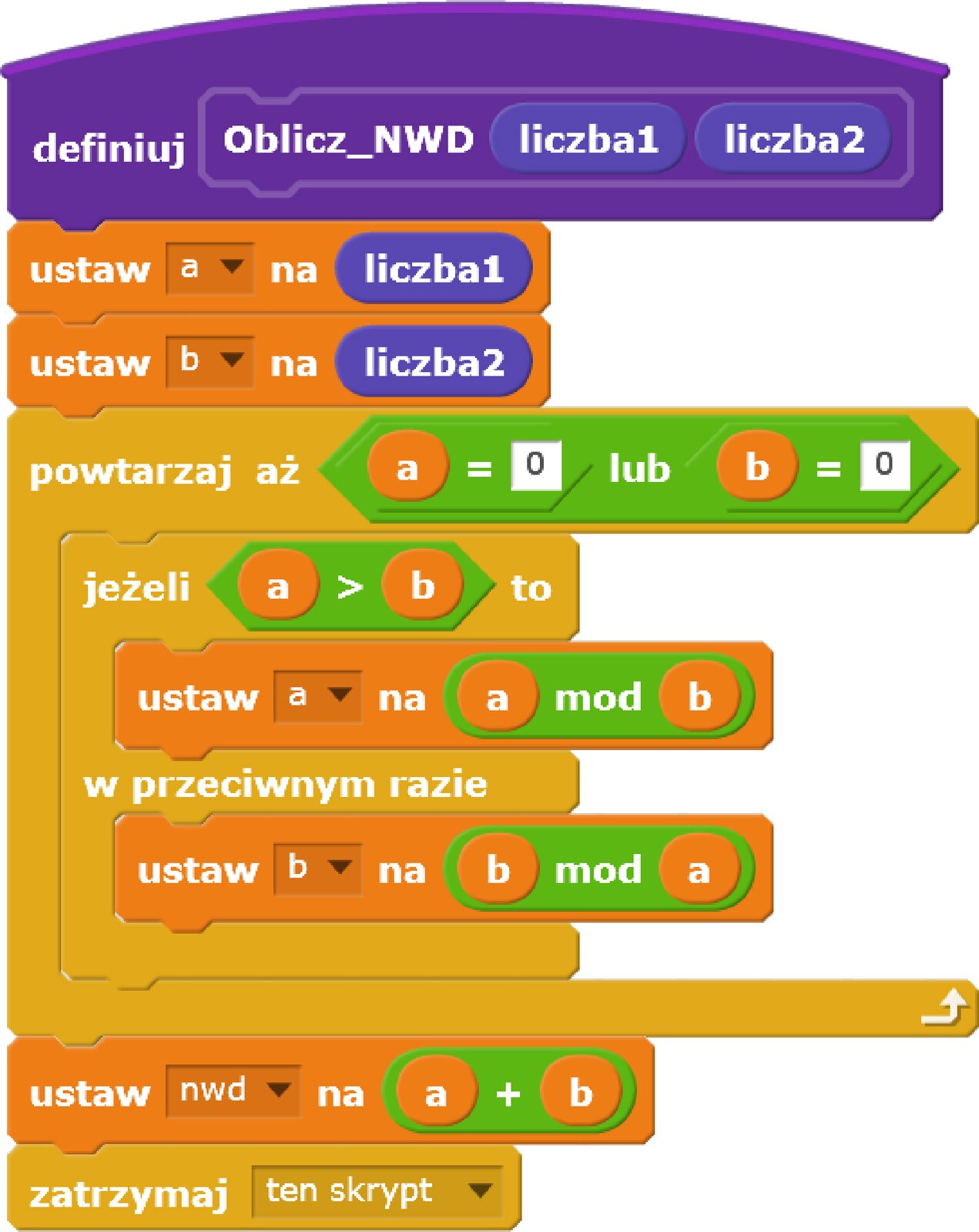
Zwróć uwagę, że jeżeli jedna liczba jest dużo większa od drugiej, to wielokrotnie będzie następowało odejmowanie od niej tej samej mniejszej liczby. Takie wielokrotne odejmowanie można zastąpić dzieleniem, a dokładniej resztą z dzielenia większej liczby przez mniejszą. Na przykład dla a=256 i b=48 otrzymujemy:


Zwróć uwagę, że zastępując odejmowanie braniem reszty z dzielenia inny jest warunek końca powtarzania: jedna z wartości osiągnie wartość 0.
Zapisz w postaci listy kroków algorytm Euklidesa znajdowania największego wspólnego dzielnika dwóch liczb całkowitych dodatnich (z wykorzystaniem reszty z dzielenia).
Znasz już kilka algorytmów znajdowania największego wspólnego dzielnika. Zastanów się, przedyskutuj ewentualnie z kolegami i koleżankami, który z nich wykona najmniej operacji, a więc będzie najbardziej efektywny.
Stwórz własny blok z dwoma parametrami liczbowymi realizujący któryś z tych algorytmów. Jeśli nie wiesz, jak tworzyć własne bloki, kliknij tutajtutaj.
Scratch chroni wartość parametrów, czyli nie można zmieniać ich wartości. Należy więc utworzyć dwie pomocnicze zmienne (dostępne tylko dla danego duszka), które będą miały na początku takie same wartości jak parametry i na których skrypt będzie dokonywał obliczeń. Podobnie, trzeba utworzyć zmienną, w której zapamiętasz wynik obliczeń.
Modyfikujemy projekt
Modyfikacja projektu będzie polegała na tym, aby rozpoznawać trzy stany:
Grający udzielił poprawnej odpowiedzi i skrócił ułamek, jeśli to możliwe.
Grający udzielił poprawnej odpowiedzi co do wartości ułamka, ale go nie skrócił.
Grający udzielił błędnej odpowiedzi.
Czy grający udzielił prawidłowej odpowiedzi sprawdzisz używając tego samego warunku, co dotychczas.

Jeśli przyjmuje on wartość prawda, należy korzystając z bloku obliczającego NWD rozstrzygnąć, czy wyświetlić „Brawo!” (stan 1), czy „Dobrze, ale można skrócić ułamek...” (stan 2).
Sformułuj warunek logiczny sprawdzający, czy grający podał jako odpowiedź skrócony ułamek.
Popraw skrypt sprawdzający odpowiedź.
Zadania uzupełniające
Dane: Prostokąt o szerokości s i wysokości w.
Wynik: Minimalna liczba takich samych kwadratów, którymi można wypełnić prostokąt.
Na przykład dla s=250 i w=150 minimalna liczba kwadratów wynosi 15 (długość boku kwadratu wynosi 50).
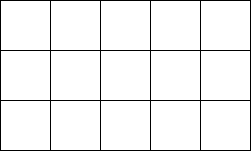
Zapisz w postaci listy kroków algorytm obliczenia minimalnej liczby kwadratów.
Przygotuj projekt, w którym duszek prosi o podanie szerokości i wysokości prostokąta oraz rysuje prostokąt wypełniony minimalną liczbą kwadratów.