Wyznaczanie gęstości ciał stałych za pomocą wagi i linijki
Czy można wyznaczyć gęstość za pomocą wagi i linijki? Czy jest to możliwe w przypadku każdego ciała o dowolnym kształcie? Jeśli chcesz poznać odpowiedzi na te pytania, czytaj dalej.

stwierdzić, że masa jest miarą ilości materii;
podać definicję objętości, jaką zajmuje ciało;
obliczyć gęstość za pomocą odpowiedniego wzoru;
odczytać gęstość substancji za pomocą tablic fizycznych.
wyznaczać eksperymentalnie gęstość ciał o regularnych kształtach, np. prostopadłościanu, walca i kuli.
kauczukową piłeczkę o średnicy nie większej niż 10 cm;
monetę jednozłotową.
1. Wyznaczanie objętości brył
Jeśli badamy ciała o regularnych kształtach, procedurę wyznaczania ich objętości możemy uprościć. W tym celu należy skorzystać z zależności matematycznych, wiążących objętość z wymiarami liniowymi badanego ciała.
Oblicz gęstość gumowej piłeczki. Masa piłeczki wynosi 15 g, a jej średnica to 3 cm.
Objętość kuli obliczamy ze wzoru:
,
gdzie: V – objętość kuli; π – liczba stała (przyjmij, że jest równa 3,14); r – promień kuli.
Przeczytaj poniższe zdania i zaznacz wszystkie poprawne odpowiedzi.
- Średnicę kulki lub walca można wyznaczyć przy użyciu trzech klocków i linijki.
- Średnicę kulki można łatwo można łatwo zmierzyć linijką.
- Średnicę kulki można wyznaczyć za pomocą suwmiarki.
Oblicz objętość walca prostego o wysokości 0,2 m i średnicy 10 cm.
Skorzystaj ze wzoru na objętość walca prostego:
,
gdzie: – objętość walca; – stała, (przyjmij, że jest równa 3,14); – promień podstawy walca.
Z dołączonego rysunku odczytaj wymiary poszczególnych części ciała i oblicz jego objętość.
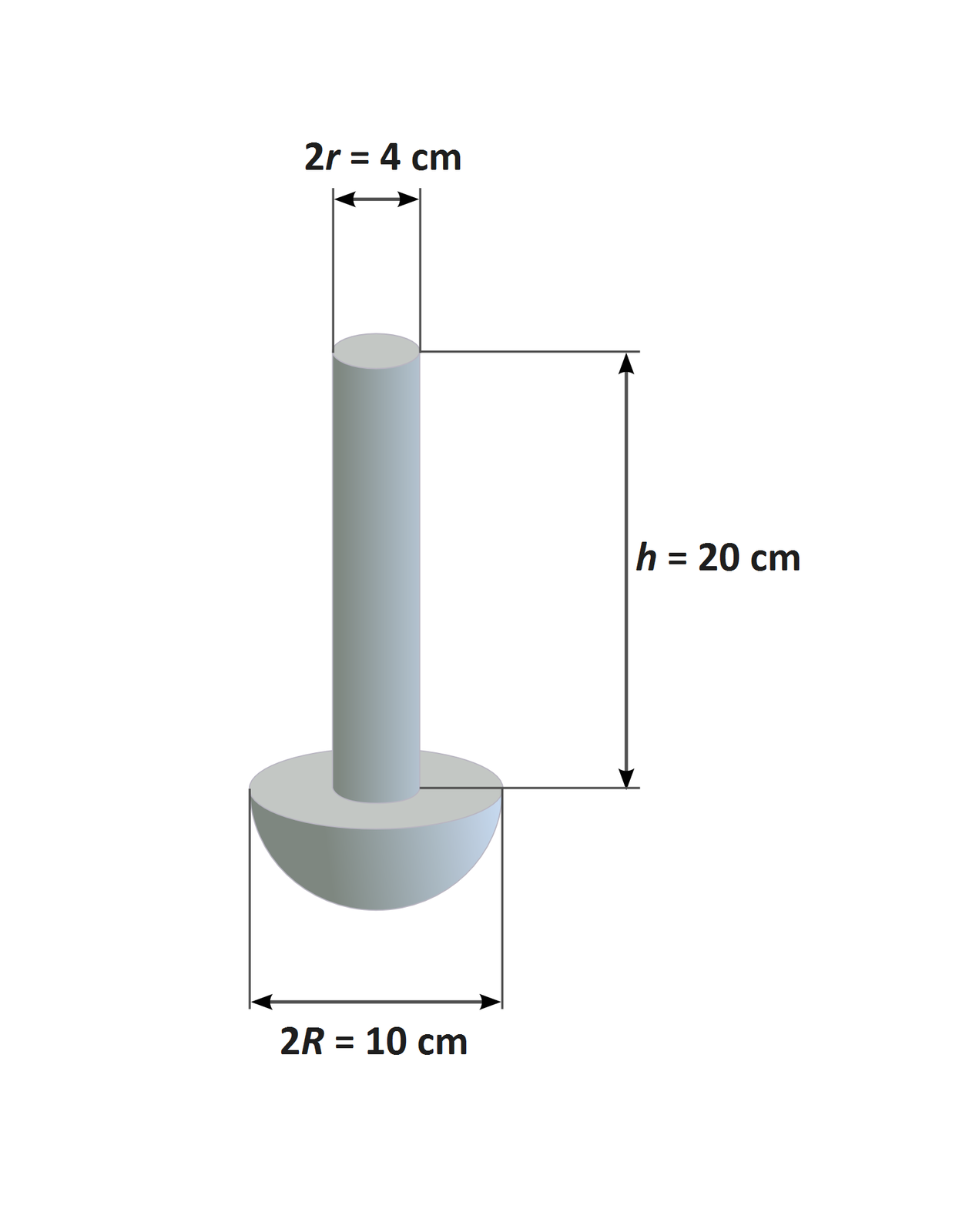
2. Wyznaczanie gęstości ciał o kształtach regularnych
Gęstość ciała wyznaczamy na postawie znajomości jego masy i objętości. Objętość otrzymujemy metodą rachunkową – do wzoru podstawiamy uzyskane wymiary ciała. Waga laboratoryjna lub mniej dokładna waga kuchenna pozwalają wyznaczyć masę ciała.
Za pomocą poniższej aplikacji wyznacz gęstość ciał.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DRwQowIvw
Wyznacz gęstość monety jednozłotowej.
Nawet jeśli nie znasz budowy wewnętrznej ciała, a chcesz wyznaczyć jego gęstość, wystarczy, że posłużysz się jedynie linijką i wagą. Otrzymasz wtedy wielkość nazywaną średnią gęstością ciała. Wnętrze przedmiotu może być niejednorodne. Oznacza to, że w jego wnętrzu mogą znajdować się wolne przestrzenie (kawerny) wypełnione gazem, które są przyczyną odchylenia pomiędzy rzeczywistą a przewidywaną masą ciała.
3. Obliczanie objętości i masy
W jaki sposób możesz wyznaczyć objętość ciała, jeśli znasz jego gęstość?
,
gdzie:
m – masa;
d – gęstość;
V – objętość.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DRwQowIvw
Wyznacz masę powietrza w swojej sali lekcyjnej. Jeśli nie jesteś w stanie wyznaczyć jej wymiarów, poproś o pomoc nauczyciela. Gęstość powietrza odczytaj z tablic fizycznych.
Pewien kierowca zapłacił za tankowanie samochodu 65 zł. Cena benzyny, którą nalał do baku auta, wynosiła 5,20 zł za litr.
Wykaż, że kierowca za 65 zł kupił benzyny.
Oblicz masę zakupionej benzyny, jeżeli jej gęstość wynosi .
Jeśli pływak ma płuca wypełnione powietrzem, może unosić się swobodnie tuż pod powierzchnią wody (np. w basenie). Gdy wydycha powietrze, zaczyna się zanurzać. Oblicz pojemność płuc pływaka. Przyjmij, że zmiana masy jego ciała wyniosła 3,87 g. Gęstość powietrza odczytaj z tablic fizycznych.
4. Niepewność wyniku pomiaru
Wykonaj z kolegami i koleżankami z klasy następujące doświadczenie: za pomocą linijki o długości 20 cm zmierzcie długość stołu. Niech każda z osób zapisze wynik swojego pomiaru i nie informuje pozostałych kolegów o zanotowanej wartości. Gdy wykonacie zadanie, wypiszcie wyniki na tablicy. Zwróćcie uwagę, że różnią się one od siebie. Dlaczego tak się stało?
Wynik każdego pomiaru różni się od rzeczywistej wartości wielkości mierzonej. Mówimy, że wynik każdego pomiaru fizycznego obarczony jestniepewnością pomiarowąniepewnością pomiarową. Wynika ona zarówno z metody samego pomiaru, jak i z dokładności użytego przyrządu.
Zastanówcie się, dlaczego uzyskane wyniki nie są jednakowe. Zaproponujcie sposób, który dałby mniejsze rozbieżności.
Wiesz już, że wyniki wszystkich pomiarów są odczytywane z pewną dokładnością. Pomiar długości lub średnicy, wykonywany za pomocą linijki ze skalą milimetrową daje wynik z dokładnością do 1 milimetra. Jeżeli oceniasz, że średnica kulki wynosi 2,5 cm, to tak naprawdę mieści się ona w granicach od 2,4 cm do 2,6 cm. Podobny problem wystąpi przy pomiarze masy. Powiedzmy, że waga kuchenna ma podziałkę, w której odległości między sąsiednimi kreskami odpowiadają 2 g. W tej sytuacji można przyjąć, że niepewność wyznaczenia masy wynosi 2 g. Czyli masa np. kulki mieści się w granicach między 68 g a 64 g. Jeśli podczas obliczania gęstości kulki przyjmiesz, że średnica kulki jest równa 2,5 cm, a masa – 66 g, nie uzyskasz prawdziwego wyniku. W jakich granicach zawiera się prawidłowy wynik gęstości kulki? Wzór na gęstość to . Jest to ułamek, którego maksymalna wartość osiągana jest wtedy, gdy jego licznik jest maksymalny, a mianownik minimalny. Jeżeli zatem chcemy wyznaczyć maksymalną wartość gęstości, to do obliczeń podstawiamy maksymalną wartość wyznaczonej masy i minimalną wartość wyznaczonej objętości (czyli bierzemy pod uwagę minimalny promień). Przedstawiono to w poniższej tabelce:
Minimalny promień | Maksymalny promień | Minimalna masa | Maksymalna masa | Minimalna objętość | Maksymalna objętość |
Jak zatem wynika z naszych obliczeń (koniecznie je sprawdź!), prawdziwa wartość gęstości kulki mieści się w granicach od do . Zwróć uwagę, że wszystkie dane oraz wyniki zapisywaliśmy z jednakową dokładnością - dokładnością do 2 cyfr znaczących.
Które odpowiedzi są prawdziwe, a które fałszywe? Zaznacz prawdziwe.
- Nigdy nie jesteśmy w stanie przeprowadzić idealnie dokładnego pomiaru fizycznego.
- Niepewność pomiaru wszystkich użytych przyrządów pomiarowych w danym eksperymencie będzie miała wpływa na końcowy wynik eksperymentu.
- Przy użyciu bardzo dokładnej linijki jesteśmy w stanie otrzymać bezbłędny wynik pomiaru.
Podsumowanie
W przypadku ciał o regularnych kształtach procedurę wyznaczania objętości można uprościć. W tym celu należy skorzystać z zależności matematycznych, wiążących objętość z wymiarami liniowymi badanego ciała.
Chcąc wyznaczyć gęstość ciała, musimy zmierzyć jego masę i objętość oraz skorzystać ze wzoru:
;
Jeśli znamy gęstość i objętość ciała, możemy obliczyć jego masę. W tym celu korzystamy ze wzoru:
;
Objętość ciała o znanej masie i gęstości obliczamy za pomocą wzoru:
;
Wynik pomiaru różni się od rzeczywistej wartości wielkości mierzonej. Mówimy, że wynik każdego pomiaru fizycznego obarczony jestniepewnością pomiarowąniepewnością pomiarową. Ta niepewność wynika zarówno z metody samego pomiaru, jak i dokładności użytego przyrządu. Przyczyną może być także niedokładne odczytanie wyników na skali przyrządu.
Na niepewność pomiaru mają także wpływ cechy przedmiotu badań.
Wyznacz gęstość mleka.
Wybierz szklankę w kształcie walca. Za pomocą wagi wyznacz masę pustej szklanki. Napełnij ją mlekiem do mniej więcej 3/4 objętości i ponownie wyznacz masę. Za pomocą linijki dokonaj pomiaru wymiarów, które pozwolą na obliczenie objętości mleka.
Zajrzyj do zagadnień pokrewnych:
Pomiary w fizyce. Niepewność pomiaru. Przeliczanie wielokrotności i podwielokrotnościPomiary w fizyce. Niepewność pomiaru. Przeliczanie wielokrotności i podwielokrotności
Zadania
Arek, Justyna i Monika rozmawiają o tym, czym jest objętość. Zapoznaj się z opinią każdej z osób i zaznacz wszystkie poprawne odpowiedzi.
- Arek: objętość to wielkość przestrzeni zajmowanej przez ciało.
- Justyna: objętość to ilość płynu, jaka może zmieścić się w środku bryły.
- Monika: objętość to ilość powietrza, jaka może zmieścić się wewnątrz ciała.
Które informacje są prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Nie da się wyznaczyć gęstości ciała o regularnych kształtach przy użyciu wagi i linijki. | □ | □ |
| Objętość ciała o regularnych kształtach można wyznaczyć mierząc objętość wypartej przez to ciało cieczy. | □ | □ |
| Bez użycia skomplikowanej aparatury badawczej nie jesteśmy w stanie wyznaczyć gęstości ciała o regularnych kształtach. | □ | □ |
Słowniczek
mówimy, że wynik każdego pomiaru fizycznego obarczony jest niepewnością pomiarową. Ta niepewność wynika zarówno z metody samego pomiaru, jak i dokładności użytego przyrządu. Przyczyną może być także niedokładne odczytanie wyników na skali przyrządu. Na niepewność pomiaru mają także wpływ cechy przedmiotu badań.