Narysuj ostrosłup prawidłowyostrosłup prawidłowyostrosłup prawidłowy czworokątny i zaznacz w nim kąt między płaszczyzną podstawy a ścianą boczną ostrosłupa. Wiedząc, że wysokość ostrosłupa jest trzy razy krótsza od wysokości jego ściany bocznej, oblicz miarę kąta liniowego zaznaczonego kąta dwuściennegokąt między płaszczyznami (kąt dwuścienny)kąta dwuściennego.

Rozwiązanie:

Zaczniemy oczywiście od rysunku:

R1KcCZakg9i87

Ilustracja przedstawia ostrosłup prawidłowy czworokątny $ABCDW$. Wysokość ostrosłupa, mająca długość H, upuszczona jest na spodek wysokości oznaczony literą S. Wysokość ściany bocznej $BCW$ upuszczona jest na krawędź BC w punkcie F i ma długość h. Kolorem różowym wyróżniono trójkąt $FSW$. Kąty BFS i CFS są kątami prostymi. Kąt $WSF$ jest kątem prostymi. Natomiast kąt $SFW$ ma miarę $\alpha$.

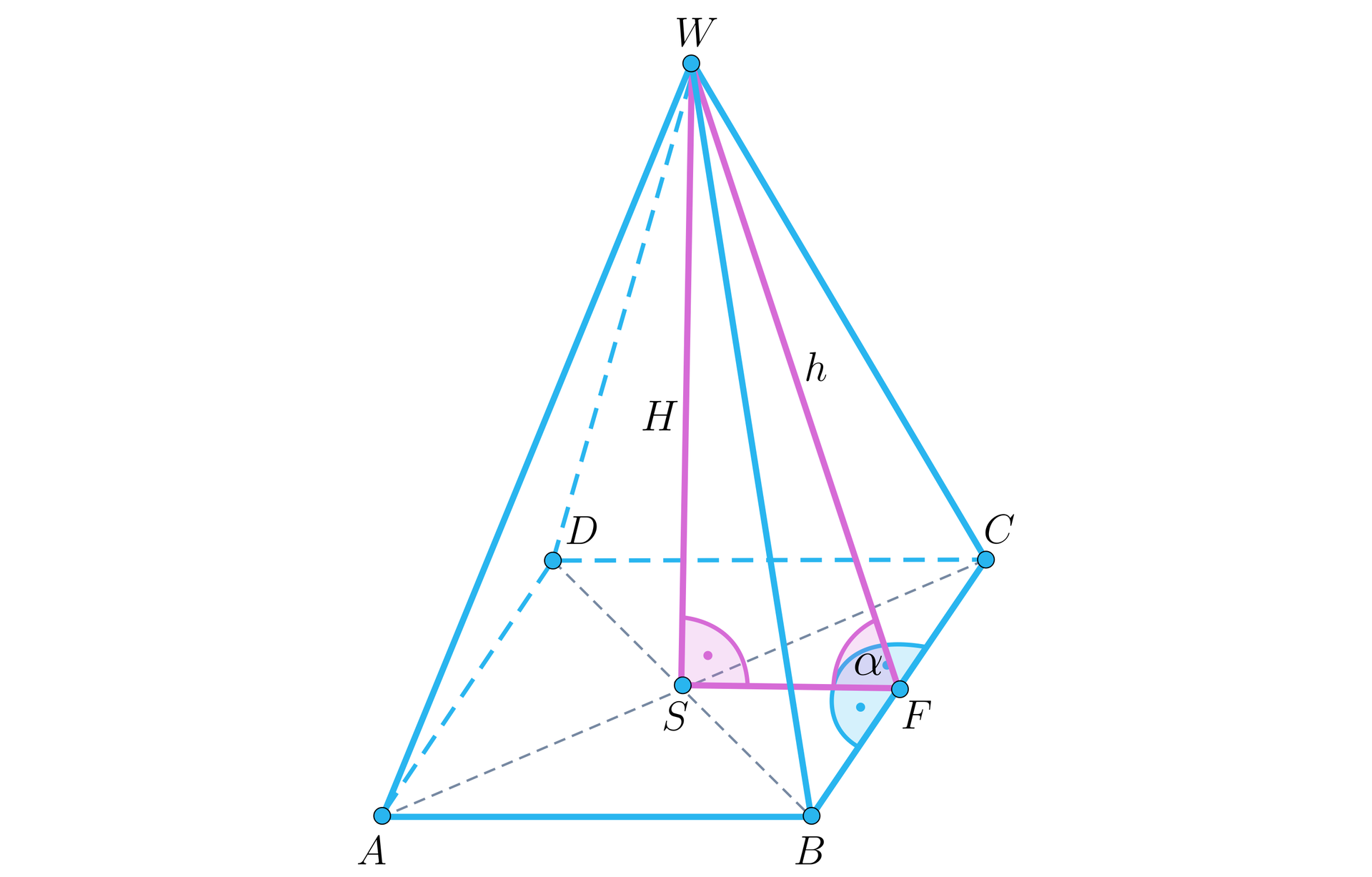
Aby zaznaczyć kąt między płaszczyzną podstawy a płaszczyzną ściany bocznej ostrosłupa, określamy najpierw prostą wspólną dla tych dwóch płaszczyzn.

Dla ściany bocznej $BCW$ jest to oczywiście prosta $BC$.

Kąt liniowykąt liniowy kąta dwuściennegoKąt liniowy naszego kąta dwuściennego można zatem zaznaczyć jako kąt między wysokością ściany bocznej prostopadłą do krawędzi podstawy ostrosłupa a odcinkiem podstawy $SF$ prostopadłym do tej samej krawędzi.

Aby wyznaczyć miarę tego kąta wystarczy wykorzystać definicję funkcji trygonometrycznej sinus w trójkącie prostokątnym $WSF$:

$\frac{\left|WS\right|}{\left|WF\right|}=\sin \alpha$

$\frac{x}{3x}=\sin \alpha$

$\frac{1}{3}=\sin \alpha$

$0,3333\approx \sin \alpha$

Wykorzystując tablice matematyczne możemy podać już miarę kąta, o który pytają w zadaniu: $\left|\measuredangle WFS\right|\approx 19°$. Odpowiedź jest przybliżona ze względu na wykorzystanie tablic trygonometrycznych.

W ostrosłupie prawidłowym czworokątnym $ABCDW$ o podstawie $ABCD$ krawędź podstawy $AB$ jest równa $15$, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę $120°$. Oblicz sumę długości wszystkich krawędzi tego ostrosłupa.

Rozwiązanie:

Zacznijmy ponownie od rysunku bryły.

R1GlMwtcCr4Qw

Ilustracja przedstawia ostrosłup prawidłowy czworokątny $ABCDW$. Wysokość ostrosłupa upuszczona jest na spodek wysokości oznaczony literą S i leżący na przecięciu przekątnych kwadratu w podstawie. Wysokość ostrosłupa ma długość H. Kąt nachylenia wysokości do płaszczyzny podstawy to $90°$. Na krawędzi bocznej CW zaznaczony został punkt G. Powstał trójkąt $BGD$, który wyróżniono kolorem różowym. Kąt przy wierzchołku G w tym trójkącie ma miarę $\alpha$. Natomiast kąty $DGW$ oraz $BGC$ są kątami prostymi.

W przypadku ostrosłupa prawidłowego wszystkie ściany boczne są przystającymi trójkątami równoramiennymi.

Stąd długości wysokości $BG$ oraz $DG$ ścian bocznych są identyczne.

Ponieważ dodatkowo przekątna kwadratu $ABCD$ o boku długości $15$ to odcinek $BD$ o długości $15\sqrt{2}$, możemy wykorzystać twierdzenie cosinusów, by obliczyć opisaną wcześniej wysokość ściany bocznej.

Wykorzystamy twierdzenie cosinusówtwierdzenie cosinusówtwierdzenie cosinusów w trójkącie $DGB$:

${\left|BD\right|}^2=x^2+x^2-2·x·x·\cos \measuredangle DGB$

${\left(15\sqrt{2}\right)}^2=2x^2-2x^2\cos 120°$

$450=2x^2+2x^2\cos 60°$

$450=2x^2+2x^2·\frac{1}{2}$

$450=3x^2$

$x=\sqrt{150}$

$x=5\sqrt{6}$.

Zauważmy teraz, że trójkąt $SGC$ jest podobny do trójkąta $WSC$.

Istotnie, oba są trójkątami prostokątnymi o wspólnym kącie ostrym przy wierzchołku $C$.

Wystarczy zatem obliczyć długość odcinka $GS$ i potem $GC$, aby wyznaczyć długość krawędzi bocznej ostrosłupa.

Długość $GS$ obliczymy z trójkąta prostokątnego $GSB$:

$\frac{\left|BS\right|}{\left|GS\right|}=\mathrm{tg}\frac{120°}{2}$

$\frac{\frac{15\sqrt{2}}{2}}{\left|GS\right|}=\mathrm{tg}60°$

$\frac{15\sqrt{2}}{2\left|GS\right|}=\sqrt{3}$

$2\sqrt{3}\left|GS\right|=15\sqrt{2}$

$\left|GS\right|=\frac{15\sqrt{2}}{2\sqrt{3}}$

$\left|GS\right|=\frac{15\sqrt{6}}{6}$.

Rozpatrzmy teraz tylko część przekroju ostrosłupa, trójkąt $WSC$

R17C61hxIItTa

Ilustracja przedstawia trójkąt prostokątny $WSC$. Pionowa przyprostokątna WS ma długość H. Z wierzchołka kąta prostego, przy wierzchołku S poprowadzona jest wysokość padająca na przeciwprostokątną CW w punkcie G. Ma ona długość d. Ponadto zaznaczono również miarę kąta $SGW$ czyli $90°$.

W tym trójkącie znamy $\left|GS\right|=\frac{15\sqrt{6}}{6}$ oraz $\left|SC\right|=\frac{15\sqrt{2}}{2}$.

Z twierdzenia Pitagorasa możemy obliczyć długość $GC$:

${\left|GC\right|}^2={\left|SC\right|}^2-{\left|GS\right|}^2$

${\left|GC\right|}^2={\left(\frac{15\sqrt{2}}{2}\right)}^2-{\left(\frac{15\sqrt{6}}{6}\right)}^2$

${\left|GC\right|}^2=\frac{225}{2}-\frac{225}{6}$

${\left|GC\right|}^2=\frac{450}{6}$

$\left|GC\right|=\sqrt{75}$

$\left|GC\right|=5\sqrt{3}$.

Ostatecznie wykorzystując podobieństwo trójkątów $SGC$ oraz $WSC$ możemy obliczyć długość krawędzi bocznej $CW$ ostrosłupa:

$\frac{\left|GC\right|}{\left|SC\right|}=\frac{\left|SC\right|}{\left|CW\right|}$

$\left|CW\right|=\frac{{\left|SC\right|}^2}{\left|GC\right|}$

$\left|CW\right|=\frac{{\left(\frac{15\sqrt{2}}{2}\right)}^2}{5\sqrt{3}}$

$\left|CW\right|=\frac{\frac{225}{2}}{5\sqrt{3}}$

$\left|CW\right|=\frac{225}{10\sqrt{3}}$

$\left|CW\right|=\frac{15\sqrt{3}}{2}$.

Zgodnie z poleceniem, mamy obliczyć sumę wszystkich krawędzi ostrosłupa. Ponieważ ostrosłup czworokątny ma cztery krawędzie podstawy i cztery krawędzie boczne, otrzymujemy ostateczny wynik:

$s=4·15+4·\frac{15\sqrt{3}}{2}=60+30\sqrt{3}$

Podstawą ostrosłupa jest czworokąt $ABCD$. Wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod kątem $\alpha$. Uzasadnij, że spodek wysokości tego ostrosłupa pokrywa się z punktem przecięcia się dwusiecznych kątów wewnętrznych danego czworokąta.

Rozwiązanie:

Zacznijmy od rysunku:

RhtGM9R4qxyfp

Ilustracja przedstawia ostrosłup czworokątny $ABCDW$. Wysokość ostrosłupa upuszczona jest na spodek wysokości, oznaczony literą S. Na krawędzi podstawy AD zaznaczono punkt M tak, że kąt $SMA$ to kąt prosty. Kolorem różowym wyróżniono trójkąt $MSW$. Kąt wewnętrzy tego trójkąta, $SMW$ ma miarę $\alpha$.

Przeanalizujemy najpierw kąt nachylenia ściany bocznej $ADW$ do podstawy ostrosłupa.

Wspólną prostą dla płaszczyzn zawierających te ściany jest prosta $AD$.

Prowadzimy płaszczyznę zawierającą wysokość $WS$ ostrosłupa, prostopadłą do prostej $AD$.

Jeżeli punkt $S$ będzie spodkiem wysokości ostrosłupa, to otrzymujemy odcinek $SM$ prostopadły do boku $AD$ czworokąta podstawy oraz odcinek $MW$ na ścianie bocznej.

Mamy zatem trójkąt prostokątny $WSM$, którego kąt wewnętrzny $SMW$ jest kątem liniowym kąta dwuściennegokąt między płaszczyznami (kąt dwuścienny)kąta dwuściennego między płaszczyzną podstawy i ścianą boczną $ADW$ ostrosłupa.

Wynika stąd, że $\mathrm{tg}\alpha =\frac{\left|WS\right|}{\left|SM\right|}$.

Analogicznie postępujemy dla kolejnych ścian bocznych ostrosłupa i otrzymujemy podobny wynik.

Jedyną zmienną w powyższej równości jest punkt $M$, który będzie definiowany kolejno jako $N$, $O$, $P$ i należał do kolejnych krawędzi podstawy ostrosłupa.

Na rysunku sytuację możemy przedstawić następująco:

R1c6ALKYJolMV

Ilustracja przedstawia ostrosłup czworokątny $ABCDW$. Wysokość ostrosłupa upuszczona jest na spodek wysokości, oznaczony literą S. Na krawędzi podstawy AD zaznaczono punkt M. Na krawędzi AB punkt mamy P, na krawędzi BC mamy punkt O, na krawędzi CD mamy punkt N. Zaznaczono również kąty wewnętrze: $SPW$, $SOW$, $SNW$ oraz $SMW$ , mające miarę $\alpha$. Wszystkie nowo powstałe trójkąty wyróżniono kolorem różowym.

Dowodzi to, że spodek wysokości ostrosłupa znajduje się w równej odległości od wszystkich boków czworokąta $ABCD$ i odległość ta jest równa $\left|MS\right|=\left|NS\right|=\left|OS\right|=\left|PS\right|=\frac{\left|WS\right|}{\mathrm{tg}\alpha }$.

Oznacza to, że do czworokąta można wpisać okrąg (istnieje punkt równo odległy od wszystkich boków czworokąta). Jak wiadomo, środek tego okręgu jest punktem przecięcia dwusiecznych kątów wewnętrznych czworokąta.

W ostrosłupie wypukłym spodek wysokości jest środkiem okręgu wpisanego w podstawę wtedy i tylko wtedy, gdy wszystkie ściany boczne tego ostrosłupa są nachylone pod tym samym kątem do płaszczyzny podstawy.

Podstawą ostrosłupa jest trapez równoramienny $ABCD$, w którym $\left|AB\right|=a$, $\left|CD\right|=b$. Wszystkie ściany boczne tego ostrosłupa są nachylone do płaszczyzny podstawy pod tym samym kątem $\alpha$. Uzasadnij, że wysokość tego ostrosłupa wyraża się wzorem $H=\frac{\sqrt{ab}}{2}\mathrm{tg}\alpha$.

Rozwiązanie:

Przyjmijmy następujące oznaczenia dla ostrosłupa:

RsuQ3hBY04mEV

Ilustracja przedstawia ostrosłup czworokątny $ABCDW$. Wysokość ostrosłupa upuszczona jest na spodek wysokości, oznaczony literą S. Na krawędzi podstawy AD zaznaczono punkt M tak, że kąt $SMA$ , to kąt prosty. Kolorem różowym wyróżniono trójkąt $MSW$. Kąt wewnętrzy tego trójkąta, $SMW$ ma miarę $\alpha$.

Ponieważ wszystkie ściany boczne są nachylone do podstawy pod tym samym kątem, to w podstawę ostrosłupa można wpisać okrąg, a spodek wysokości ostrosłupa jest środkiem tego okręgu.

Przeanalizujmy zatem samą podstawę ostrosłupa:

R2v6mqUuKXN5w

Ilustracja przedstawia podstawę ostrosłupa będącą trapezem równoramiennym. Górna podstawa CD długość b, prawy oraz lewy ukośny bok długość m. Z lewego oraz prawego górnego wierzchołka upuszczono na podstawę wysokości h i oznaczono kąty proste między tymi wysokościami a podstawą. Zaznaczono również punkty na krawędzi podstawy, w miejsce których zostały upuszczone wysokości. Odpowiednio punkt E dla wysokości wychodzącej z punktu D oraz punkt F dla tej z punktu C. Odcinek EF ma długość b.

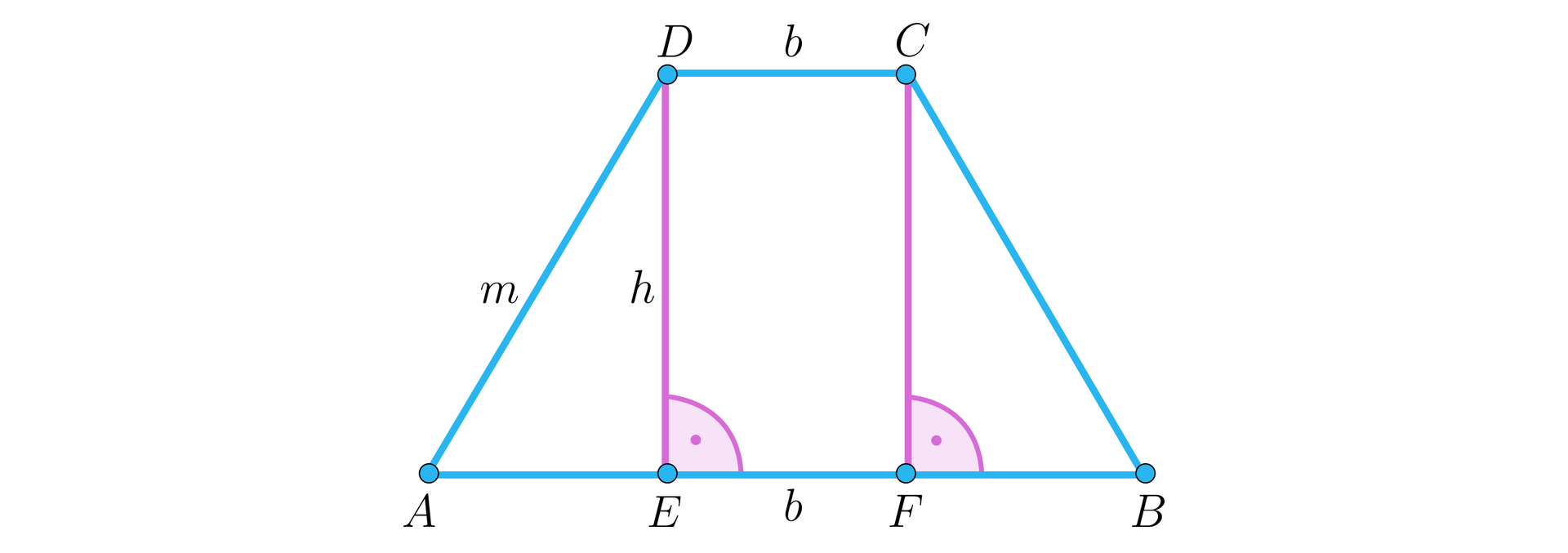
Z warunku czworokąta opisanego na okręgu wynika, że suma ramion $m$ trapezu jest równa sumie jego podstaw, stąd:

$2m=a+b$

$m=\frac{a+b}{2}$

Jeżeli zauważymy teraz, że gdy podstawa $AB$ trapezu ma długość $a$ oraz odcinek $EF$ tej podstawy ma długość $b$, to z faktu, że trapez jest równoramienny wynika, że odcinek $AE$ trapezu $ABCD$ ma długość $\frac{a-b}{2}$.

Możemy wykorzystać twierdzenie Pitagorasa dla trójkąta $AED$, by obliczyć wysokość $h$ trapezu:

$h^2+{\left(\frac{a-b}{2}\right)}^2={\left(\frac{a+b}{2}\right)}^2$

$h^2=\frac{a^2+2ab+b^2-a^2+2ab-b^2}{4}$

$h^2=ab$

$h=\sqrt{ab}$

Promień okręgu wpisanego w trapez jest połową jego wysokości, zatem:

$r=\frac{\sqrt{ab}}{2}$

Ostatecznie wykorzystując w ostrosłupie trójkąt $WSM$ otrzymujemy długość wysokości ostrosłupa:

$\frac{H}{r}=\mathrm{tg}\alpha$

$H=r·\mathrm{tg}\alpha$

$H=\frac{\sqrt{ab}}{2}\mathrm{tg}\alpha$.

każda z dwóch części przestrzeni, na jakie dzielą ją dwie półpłaszczyzny, nazywane ścianami kąta dwuściennego, mające wspólną krawędź nazywaną krawędzią kąta dwuściennego, wraz z punktami każdej półpłaszczyzny

kątem liniowym kąta dwuściennego nazywa się kąt płaski będący częścią wspólną tego kąta dwuściennego oraz płaszczyzny prostopadłej do jego krawędzi

miarą kąta dwuściennego nazywa się miarę jego dowolnego kąta liniowego (wszystkie są przystające)

twierdzenie określające związek między kątem wewnętrznym trójkąta i bokami tego trójkąta:

w dowolnym trójkącie kwadrat długości jednego z boków jest równy sumie kwadratów długości pozostałych dwóch boków pomniejszonej o podwojony iloczyn tych boków i cosinusa kąta między nimi zawartego

ostrosłupem prawidłowym nazywamy taki ostrosłup prosty, którego podstawa jest wielokątem foremnym