Przeczytaj

W temacie tym zajmiemy się funkcjami, które są określone na kliku różnych przedziałach poprzez różne funkcje elementarefunkcje elementarnefunkcje elementare. Jak wiemy funkcje elementarnefunkcje elementarnefunkcje elementarne posiadają granicę w każdym punkcie swojej dziedziny oraz granica ta jest równa wartości funkcji w tym punkcie. W związku z tym badając granice funkcji określonych różnymi wzorami na kilku przedziałach wystarczy ograniczyć się do badania granicy w punktach, w których funkcja „zmienia swój wzór”. W argumentach należących do wnętrza każdego z przedziałów granica będzie równa wartości funkcji liczonej według wzoru, którym funkcja jest określona na tym przedziale. Przy obliczaniu granicy w punktach, w których funkcja zmienia wzór, korzystać będziemy z poniższego twierdzenia.

o istnieniu granicy funkcji w punkcie

Twierdzenie: o istnieniu granicy funkcji w punkcie

Jeśli funkcja $f : D_{f} \to ℝ$ posiada w punkcie $x_0\in\mathbb{R}$ granicę lewo- oraz prawostronną oraz granice te są równe, to wówczas posiada ona także granicę w tym punkcie oraz

$\lim\limits_{x\to x_0^-}f(x)=\lim\limits_{x\to x_0^+}f(x)=\lim\limits_{x\to x_0}f(x)$

Spójrzmy na poniższe przykłady.

Przykład 1

Rozważmy funkcję

f (x) = \{\begin{cases} \begin{array}{ll} x + 1 & dla x \in (- \infty, - 2 ⟩ \end{array} \\ \begin{array}{ll} x^{2} - 1 & dla x \in (- 2, 1 ⟩ \end{array} \\ \begin{array}{ll} 1 - x & dla x \in (1, + \infty) \end{array} \end{cases}

Sprawdzimy czy posiada ona granicę w punktach $x_1=-2$ oraz $x_2=1$ . Na początek spójrzmy na wykres tej funkcji.

Rhx2xStJU5fUI

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus czterech do czterech. Na płaszczyźnie zaznaczono wykres funkcji f składający się z trzech części. Pierwsza część znajduje się z trzeciej ćwiartce. Biorąc pod uwagę poziomą oś, od minus nieskończoności do minus dwóch jest to ukośna półprosta określona w swojej dziedzinie wzorem y=x+1. Początek tej półprostej ma współrzędne -2;-1 i należy do wykresu funkcji. Druga część wykresu znajduje się w drugiej, trzeciej i czwartej ćwiartce. Jest to fragment paraboli o wierzchołku w punkcie 0;-1 i ramionach skierowanych do góry. Lewe ramię fragmentu paraboli ograniczone jest punktem -2;3, który nie należy do wykresu funkcji, natomiast koniec prawego ramienia znajduje się w punkcie 1;0. Trzecia część wykresu to ukośna półprosta leżąca w czwartej ćwiartce. Jej początek znajduje się w punkcie 1;0, a opisuje ją wzór y=1-x.

Jak widzimy funkcja jest określona różnymi wzorami na lewo oraz na prawo od danych punktów. Oznacza to, że konieczne jest obliczenie granic jednostronnych. Ponieważ na lewo od punktu $x_1=-2$ funkcja jest określona wzorem $f(x)=x+1$ więc

$\lim\limits_{x\to -2^-}f(x)=\lim\limits_{x\to -2^-}(x+1)=-2+1=-1$ .

Z drugiej strony na prawo od punktu $x_1=-2$ funkcja jest określona wzorem $f(x)=x^2-1$ więc

$\lim\limits_{x\to -2^+}f(x)=\lim\limits_{x\to -2^+}(x^2-1)=4-1=3$ .

Jak widzimy granice jednostronne funkcji $f$ w punkcie $x_1=-2$ są różne. Oznacza to, że granica funkcji $f$ w punkcie $x_1=-2$ nie istnieje. Rozważmy teraz punkt $x_2=1$ . Na lewo od tego punktu $f(x)=x^2-1$ więc

$\lim\limits_{x\to 1^-}f(x)=\lim\limits_{x\to 1^-}(x^2-1)=1-1=0.$

Z kolei na prawo od punktu $x_2=1$ mamy $f(x)=1-x$ , zatem

$\lim\limits_{x\to 1^+}f(x)=\lim\limits_{x\to 1^+}(1-x)=1-1=0.$

Jak widzimy granice jednostronne funkcji $f$ w punkcie $x_2=1$ są równe. Wynika stąd, że funkcja $f$ posiada granicę w punkcie $x_2=1$ oraz

$\lim\limits_{x\to 1}f(x)=0.$

Przykład 2

Rozważmy funkcję

f (x) = \{\begin{cases} \frac{x^{2} - x - 6}{x - 3} dla x \in ⟨ 0, 3) \\ 5 dla x \in ⟨ 3, 4 ⟩ \\ \frac{x^{2} - 3 x - 4}{x - 4} dla x \in (4, 6 ⟩ \end{cases}

Dziedziną danej funkcji jest zbiór $D_f=\langle0,6\rangle$ . Sprawdzimy czy istnieje granica funkcji $f$ w punktach $x_1=3$ oraz $x_2=4$ , w których zmienia się jej wzór. Zauważmy, że $x^2-x-6=(x-3)(x+2)$ oraz $x^2-3x-4=(x-4)(x+1)$ . W związku z tym wzór funkcji $f$ możemy zapisać w prostszej postaci

f (x) = \{\begin{cases} x + 2 dla x \in ⟨ 0, 3) \\ 5 dla x \in ⟨ 3, 4 ⟩ \\ x + 1 dla x \in (4, 6 ⟩ \end{cases} \begin{array}{l}  \end{array}

Obliczymy teraz granice jednostronne funkcji $f$ . Mamy kolejno

$\lim\limits_{x\to 3^-}f(x)=\lim\limits_{x\to 3^-}(x+2)=3+2=5.$
$\lim\limits_{x\to 3^+}f(x)=\lim\limits_{x\to 4^-}f(x)=5.$
$\lim\limits_{x\to 4^+}f(x)=\lim\limits_{x\to 4^+}(x+1)=4+1=5.$

Jak widzimy granice jednostronne funkcji $f$ w punktach $x_1=3$ oraz $x_2=4$ są równe. Wynika stąd, że funkcja $f$ posiada w obu tych punktach granicę oraz

$\lim\limits_{x\to 3}f(x)=\lim\limits_{x\to 4}f(x)=5.$

Poniżej znajduje się wykres funkcji $f$ .

R1PgFC3g9ZZ9Q

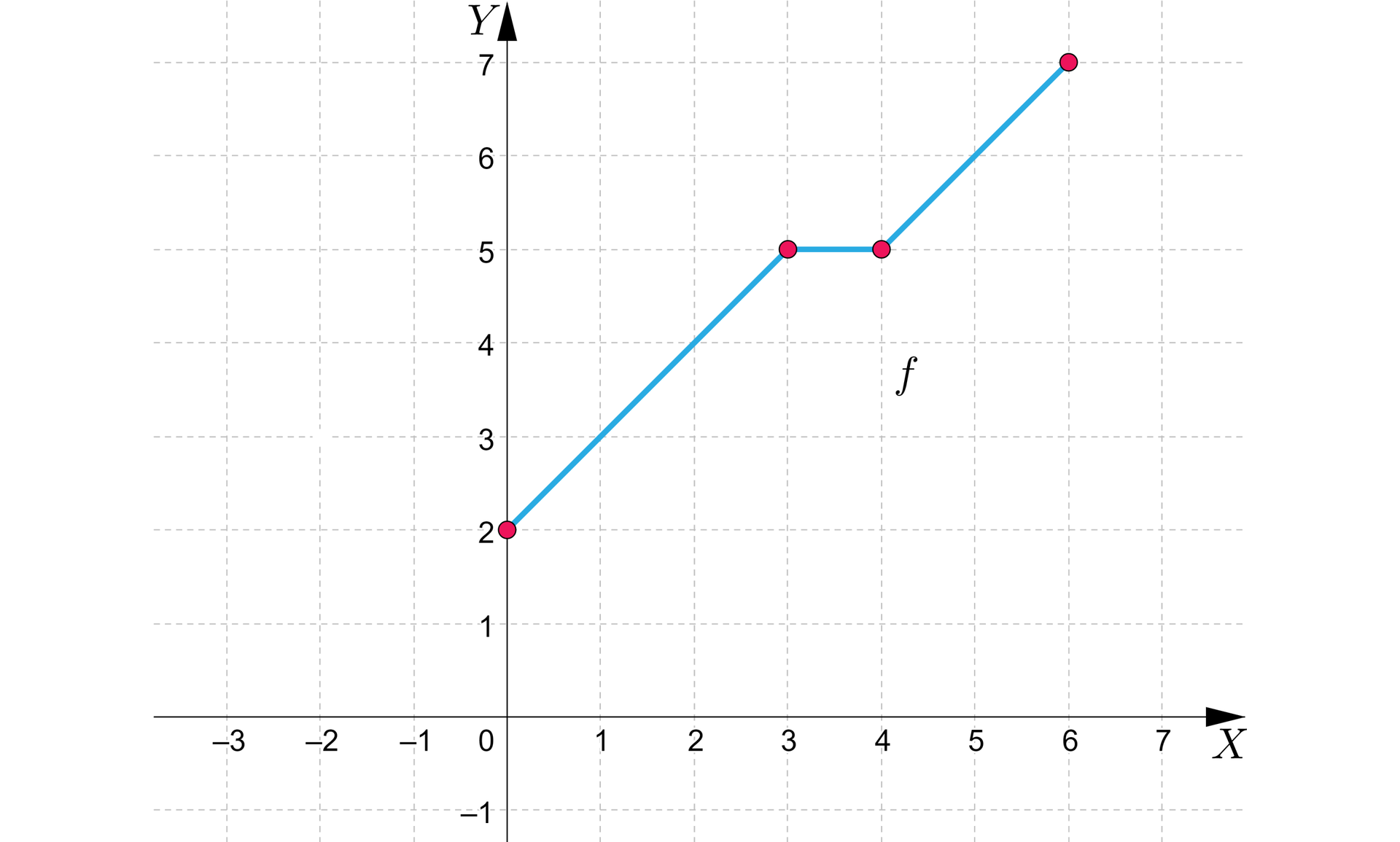
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus trzech do siedmiu oraz z pionową osią Y od minus jeden do siedmiu. Na płaszczyźnie zaznaczono wykres funkcji f składający się z trzech odcinków znajdujących się w pierwszej ćwiartce układu. Pierwsza część wykresu to ukośny odcinek o początku w punkcie 0;2 i końcu w punkcie 3;5. Punkt ten jest jednocześnie początkiem drugiego, poziomego odcinka o końcu w punkcie 4;5. Trzecia część wykresu to ukośny odcinek o początku w punkcie 4;5 i końcu w punkcie 6;7. Wszystkie końce odcinków należę do wykresu funkcji.

Przykład 3

Obliczymy granicę funkcji

f (x) = \{\begin{cases} \log_{4} x dla x \in (0, 2 ⟩ \\ x - 1 dla x \in (2, 4 ⟩ \\ 3^{2 x - 7} dla x \in (4, + \infty) \end{cases} \begin{array}{l}  \end{array}

w punktach $x_1=2$ oraz $x_2=4$ . W tym celu obliczymy granice jednostronne w tych punktach. Ponieważ na lewo od punktu $x_1=2$ mamy $f(x)=\text{log}_4x$ . więc

$\lim\limits_{x\to 2^-}f(x)=\lim\limits_{x\to 2^-}\text{log}_4x=\text{log}_42=\frac{1}{2}.$

Z kolei na prawo od punktu $x_1=2$ funkcja jest określona wzorem $f(x)=x-1$ , czyli

$\lim\limits_{x\to 2^+}f(x)=\lim\limits_{x\to 2^+}(x-1)=2-1=1.$

Jak widzimy granice jednostronne funkcji $f$ w punkcie $x_1=2$ są różne. Oznacza to, że funkcja nie posiada granicy w tym punkcie. Sprawdzimy teraz czy funkcja posiada granicę w punkcie $x_2=4$ . w tym celu liczymy granice jednostronne. Mamy

$\lim\limits_{x\to 4^-}f(x)=\lim\limits_{x\to 4^-}(x-1)=4-1=3.$

oraz

$\lim\limits_{x\to 4^+}f(x)=\lim\limits_{x\to 4^+}3^{2x-7}=3^{8-7}=3.$

W tym przypadku granice jednostronne są sobie równe co oznacza, że funkcja posiada granicę w punkcie $x_2=4$ oraz

$\lim\limits_{x\to 4}f(x)=3.$

Przykład 4

Obliczymy granicę funkcji

f (x) = \{\begin{cases} \sin x dla x \in ⟨ 0, \frac{π}{6} ⟩ \\ \cos 2 x dla x \in (\frac{π}{6}, \frac{π}{2} ⟩ \\ 1 + 2 \sin 3 x dla x \in (\frac{π}{2}, 2 π ⟩ \end{cases} \begin{array}{l}  \end{array}

w punktach $x_1=\frac{\pi}{6}$ oraz $x_2=\frac{\pi}{2}$ . Na lewo oraz na prawo od punktu $x_1=\frac{\pi}{6}$ funkcja $f$ określona jest różnymi wzorami więc liczymy granice jednostronne. Mamy

$\lim\limits_{x\to \frac{\pi}{6}^-}f(x)=\lim\limits_{x\to \frac{\pi}{6}^-}\sin x=\sin\frac{\pi}{6}=\frac{1}{2}$

oraz

$\lim\limits_{x\to \frac{\pi}{6}^+}f(x)=\lim\limits_{x\to \frac{\pi}{6}^+}\cos 2x=\cos\frac{\pi}{3}=\frac{1}{2}.$

Jak widzimy granica lewostronna funkcji $f$ w punkcie $x_1=\frac{\pi}{6}$ jest równa granicy prawostronnej w tym punkcie, zatem

$\lim\limits_{x\to \frac{\pi}{6}}f(x)=\frac{1}{2}.$

Obliczmy teraz granice jednostronne funkcji $f$ w punkcie $x_2=\frac{\pi}{2}$ . Mamy

$\lim\limits_{x\to \frac{\pi}{2}^-}f(x)=\lim\limits_{x\to \frac{\pi}{2}^-}\cos 2x=\cos\pi=-1$

oraz

$\lim\limits_{x\to \frac{\pi}{2}^+}f(x)=\lim\limits_{x\to \frac{\pi}{2}^+}(1+2\sin 3x)=1+2\sin\frac{3\pi}{2}=1-2=-1.$

W tym przypadku granice jednostronne także są równe. Wnisokujemy stąd, że funkcja $f$ posiada w punkcie $x_2=\frac{\pi}{2}$ granicę oraz

$\lim\limits_{x\to \frac{\pi}{2}}f(x)=-1.$

Słownik

funkcje elementarne

do funkcji elementarnych zaliczamy następujące funkcje

wielomiany (w szczególności funkcje liniowe i kwadratowe)
funkcje wymierne
funkcje wykładnicze
funkcje logarytmiczne
funkcje trygonometryczne
funkcje typu $f(x)=\sqrt[n]{x}$

ponadto funkcją elementarną jest suma, różnica, iloczyn, iloraz oraz złożenie dowolnych dwóch funkcji elementarnych

Wprowadzenie

Infografika

Słownik